Kepler’s law is what concerning the movement of a planet. If you can master this rule, you can easily think about the movement of the planet. And in order to think about this, it is the quickest to introduce the motion equation of two-dimensional polar coordinates. In this post, I’ll introduce Kepler’s law and prove it.
Equation of motion of two-dimensional polar coordinates
Equation of motion in radial direction
$$F_r(t)=m\left( \ddot{r}-r\dot{\varphi}^2\right)$$
Equation of motion of angular component
$$F_{\varphi}(t)=m\left( 2\dot{r}\dot{\varphi}+r\ddot{\varphi} \right)$$
To make it easy to see mathematical formulas, we often represent time derivative by adding a dot above variable like \(\dot{r}\).
Kepler’s Laws
Kepler’s first law of orbits
Each planet in solar system is moving on an elliptical orbit, with the sun as one of its focal points.
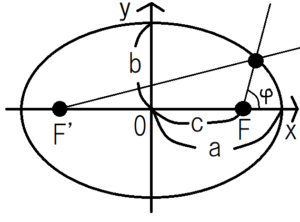
An ellipse expressed by polar coordinates becomes as follows.
$$r=\frac{l}{1+εcos{\varphi}}$$
\(ε \equiv \frac{c}{a}\):Eccentricity
\(l \equiv \frac{b^2}{a}\):semi-parameter
Kepler’s second law
The planet is moving on an elliptical orbit, with the sun as one of its focal points.
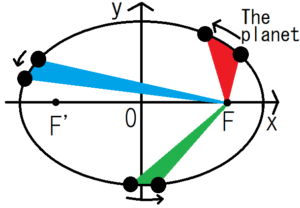
Connect the center of the planet and the focal point of the elliptical orbit \(F \) with a straight line. The area drawn by the line in unit time is constant. In other words, the areas of red, blue and green are all equal.
Kepler’s third law
The square of the revolution period of the planet is proportional to the cube of the semi-major axis \(a\) of the elliptical orbit.
$$T^2 \propto a^3$$
Exercise1 Proof of Kepler’s first law
About universal gravitation
The universal gravitation and its potential are expressed as follows.
$$f(r)=-G\frac{mM}{r^2}$$
$$U(r)=-G\frac{mM}{r}$$
Link:Universal Gravitation and Gravitational Potential
\(m\):the mass of the planet
\(M\):the mass of the Sun
Equation of motion
First of all, in this system, the angular force acting on the planet is \(0\).
$$m\left( 2\dot{r}\dot{\varphi}+r\ddot{\varphi} \right)=0…(1)$$
Paying attention to the integration by parts, the following expression holds.
The right-hand side of Equation (2) is simply the result of multiplying both sides of Equation (1) by \(\frac{r}{m}\)
$$\frac{d}{dt}(r^2\dot{\varphi})=0$$
By integrating both sides with \(t\), we obtain the following expression using constant \(h\) independent of \(t\).
$$r^2\dot{\varphi}=h…(3)$$
To express distance \(r\) with angle \(\varphi\)
Using equation (3), convert \(dr(t)/t\) into \(dr/d\varphi\).
We define u as
$$u \equiv \frac{1}{r},$$
$$du=-\frac{dr}{r^2}.$$
Therefore,
$$\frac{dr}{dt}=-h\frac{du}{d\varphi}$$
Differentiate \(\frac{dr}{dt}\) with respect to t again.
Equation of motion in the radial direction
Substitute the results so far into the equation of motion in radial direction
Specifically, substitute \(-G\frac{mM}{r^2}\) into \(F_r(t)\), \(-\frac{h^2}{r^2}\frac{d^2u}{dφ^2}\) into \(\ddot{r}\) and the equation (3) into \(\dot{φ}\).
Multiply both sides of this expression by \(\left( -\frac{r^2}{h^2m}\right)\) and then assign \(u=\frac{1}{r}\) .
If we solve this differential equation, \(u(φ)\) and \(r\) are obtained.
How to solve the differential equations
In order to solve a differential equation such as Expression (4), first find a solution considering a term that does not include variable \(u\) as \(0\). That is, the first equation we must solve is the following.
$$\frac{d^2u}{dφ^2}=-u$$
Since this differential equation is similar to that of simple harmonic motion, the solution \(u(φ)\) can be expressed as follows using initial phase \(φ_0\) and constant \(A\).
$$u(φ)=Acos(φ-φ_0)$$
Furthermore, \(u(φ)=\frac{GM}{h^2}\) that doesn’t include φ also satisfies the equation (4).
The general solution of the equation (4) is the sum of these.
$$ u(φ)=Acos(φ-φ_0)+\frac{GM}{h^2}$$
If you assign \(u=\frac{1}{r}\), r(φ) finally come out.
\(l \equiv \frac{h^2}{GM}\), \(ε \equiv \frac{h^2}{GM}A\)
\(φ_0\) represents the long axis direction.
The figure represented by the function \(r(φ)\) changes depending on the value of \(ε\). If \(ε=0\), it is a circle, ellipse if \(0<ε<1\), parabola if \(ε=1\), and hyperbola if \(ε>1\).
Exercise2 Proof of Kepler’s second law
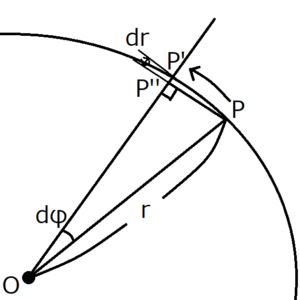
Suppose the planet moves from \(P\) to \(P’\) as shown above. The area speed at this time is \(OPP’\). To prove the second law, first find the area speed \(OPP’\) and show that this is a constant independent of t.
Draw a perpendicular line from \(P\) to the line \(OP’\) and name the intersection of them \(P”\).
When the angle \(dφ\) is small, it can be approximated as \(PP”=rdφ\). Then the area speed \(OPP’\) is as follows.
\(dr\) and \(dφ\) are assumed to be sufficiently small. Then, the second term including both of them can be regarded as sufficiently small as compared with the first term, so the second term can be ignored.
$$OPP’≒\frac{1}{2}r^2dφ$$
To find the area speed, divide the area \(OPP’\) by the time \(dt\).
We used equation (3) in Exercise1 for the last transformation. Since \(h\) is a constant independent of t, the area speed is constant.
Exercise3 Proof of Kepler’s third law
From the definition of the semi-parameter \(l \equiv \frac{b^2}{a}\), we can say \(b=\sqrt{al}\). Then from \(l=\frac{h ^ 2}{GM}\) in Exercise1, we can say \(h=\sqrt{GMl}\).
To find the period \(T\), divide the area of the ellipse \(πab\) by the area speed \(\frac{h}{2}\).
If you squaring both sides, the third law appears.
$$T^2 \propto a^3$$