1. /
  2. /
  3. Lorentz Contraction and its Derivation

Lorentz Contraction and its Derivation

Observe moving objects near the light speed from a static system. Then, the object looks shorter than the original length (the length when the object stopped). This phenomenon is called Lorentz contraction.

Let \(L_0\) be the length of the bar when the object is stopped and \(L\) the length of the moving bar observed from the static system. Then, the following relationship holds between the two. However, it is assumed that the system S’ is moving at a speed V in the x direction with respect to the system S and the bar is moving with the system S’.

\begin{eqnarray} L&=&L_0\sqrt{1-\frac{V^2}{c^2}}\\&=&L_0\sqrt{1-β^2} \end{eqnarray}

Derivation of Lorentz contraction

Review of Lorentz transformation

\begin{cases} t’=γ\left(t-\frac{V}{c^2}x \right)\\x’=γ(x-Vt)\\y’=y\\z’=z \end{cases}
$$γ=\frac{1}{\sqrt{1-\frac{V^2}{c^2}}}=\frac{1}{\sqrt{1-β^2}}$$

$$β=\frac{V}{c}$$

Link:Lorentz Transformation

Derivation of Lorentz contraction

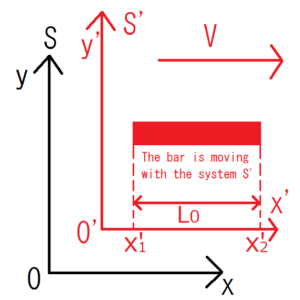
As I wrote before, let the system S’ is moving at a speed V in the x direction with respect to the static system S and the bar is moving with the system S’.

The ends of the bar in the system \(S\) are denoted by \(x_1\) and \(x_2\). Likewise, those of the bar in the system \(S’\) are denoted by \(x’_1\) and \(x’_2\). Since the bar is moving with the system \(S’\), the bar looks stationary if observers are in the system \(S’\). Therefore, the length of the bar \(x’_2-x’_1\) observed in the system \(S’\) is the same as that of the original bar \(L_ 0\).

$$x’_2-x’_1=L_0$$

I’ll show the length of the bar \(L\) observed from the static system \(S\) using \(L_0\).

First, the relationship between \(x_1\) and \(x’_1\), \(x_2\) and \(x’_2\) are as follows by Lorentz transformation.

\begin{eqnarray}  \left\{ \begin{array}{l} x’_1=γ(x_1-Vt) \\ x’_2=γ(x_2-Vt) \end{array} \right. \end{eqnarray}

After that substitute the Lorentz transformation above into \(L_0=x’_2-x’_1\).

\begin{eqnarray} L_0&=&x’_2-x’_1\\&=&(γ(x_2-Vt))-(γ(x_1-Vt))\\&=&γ(x_2-x_1)\\&=&γL \end{eqnarray}

Divide both sides by \(γ\).

$$L=L_0\sqrt{1-\frac{V^2}{c^2}}$$

Considering \(\sqrt{1-\frac{V^2}{c^2}}<1\),

$$L_0>L$$

This formula shows the length of the bar \(L\) observed from the static system \(S\) is shorter than the original length \(L_0\).

Conclusion

Observed from the static system, the moving bar looks shrinking in the direction of travel.

Leave a Reply

*

CAPTCHA