The universal gravitational force working between a particle of mass \(m\) and a particle of mass \(M\) is expressed as follows when the distance between the particles is \(r\).
$$f(r)=-G\frac{mM}{r^2}$$
$$G=6.672 \times 10^{-11}[N・m^2/kg^2]$$
\(G\) is called gravitational constant.
Universal Gravitational Potential Energy
The following relation holds for potential energy and universal gravitational force.
$$f(r)=-\frac{dU}{dr}$$
Therefore, to calculate the potential energy \(U(r)\), you should integrate the force with respect to the position \(x\). If this is adapted to universal gravitational force, the potential energy \(U(r)\) due to the universal gravitation can be expressed as follows.
$$U(r)=-G\frac{mM}{r} \cdots (1)$$
Black Hole and Interpretation of Potential
As above, the potential energy of universal gravitation becomes negative. Graph this, it looks like the figure below.
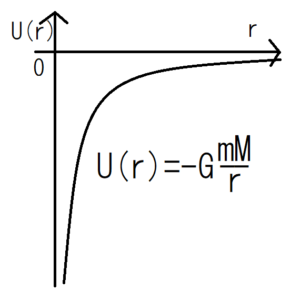
Potential energy represents the mobility of an object at that point. The lower the potential, the easier the object moves. In other words, considering the potential that the Earth creates, the closer it is to the center of the earth (r = 0), the faster the object will move toward the center of the earth. Conversely, as the object move away from the center of the Earth, the impact of the Earth’s potential will become smaller.
However, as we approach \(r=0\), the potential diverges to \(-\infty\). That means that if you get closer to \(r=0\), there will be places where the potential is too steep for the object to escape. Actually, this is the mechanism of a black hole.
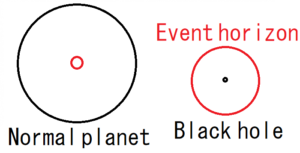
The black circles in the figure above represent the body of a planet, whereas the red circles represent the extent that even light will not be able to escape from inside of the circles. Normal objects such as the Earth and the Sun, like the left, the body itself contains a red circle. Therefore, you can escape from the Earth with a rocket or the like from its surface.
On the other hand, the body of a black hole is too dense, so the red circle is larger than the body itself. Therefore, it reaches the red circle before arriving at the surface of the body. This red circle of the black hole is called event horizon.
Exercise1 The strength of gravity
Find the strength of gravity on a 60kg person. Let the mass of the Earth be \(6.0 \times 10^{24} [kg] \) and the radius be \(R=6.4 \times 10^6[m]\).
Assume that the person is on the surface of the Earth and assign it to the formula of universal gravitation.
By the way, assigning \(m=60 [kg]\), \(g=9.8\) (gravity acceleration) to \(F=mg\) gives the following.
$$F=60×9.8≒5.9×10^2[N]$$
In this way, we can see that the force that works between the person and the Earth obtained from the universal gravitation and the force obtained from \(F=mg\) are in agreement.
Exercise2 Escape speed
We want to escape from the Earth using a rocket. When launching a rocket perpendicular to the ground surface, what is the minimum initial speed required?
Assuming the mass of the rocket as \(m\), the mechanical energy of the rocket is as follows.
Then, when we are on the ground surface, the kinetic energy is given as follows, assuming that the required initial velocity is \(v_0\) and the radius of the Earth is \(R\).
On the other hand, when the rocket reaches speed 0 at infinity, the mechanical energy of the rocket at this time becomes \ (0 \) because the potential at infinity is 0 from equation (1).
Therefore, from principle of conservation of mechanical energy, the following expression is obtained.
Therefore,
The escape speed is about 11 km per second. We can see that escape speed does not depend on mass of rocket because the rocket mass \(m\) disappears halfway.