[mathjax]
Most relativity theory book starts with Lorentz transformation. Lorentz transformation is to connect time and space of two systems that have different motion.
Unlike the classical mechanics and electromagnetism we have learned so far, the theory of relativity is incredible at first sight. For example, according to the theory of relativity, an object with mass can not catch up with the speed of light. In addition, if you are moving at a speed close to light, the time progresses slowly for you. Let’s consider the meaning of Lorentz transformation carefully by reading this article.
Expression of Lorentz Transformation
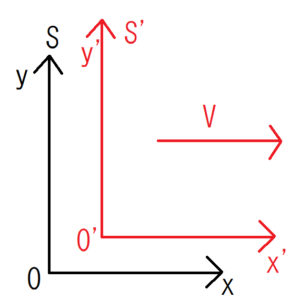
There is a system \(S’\) that is running at speed \(V\) in the \(x\) direction as seen from system \(S\). Thanks to a clock in each system, you can see that the time of the system \(S\) is \(t\) and that of the system \(S’\) is \(t’\). The coordinates of each system are represented by \(S(O-x,y,z)\) and \(S'(O’-x’,y’,z’)\).
At this time, the Lorentz transformation is expressed as follows. You can see how the system \(S’\) is seen from the system \(S\) by this conversion.
$$β=\frac{V}{c}$$
Inverse Lorentz Transformation
The inverse Lorentz transformation is to convert the system \(S’\) into the system \(S \) unlike the Lorentz transformation. You can see how the system \(S\) is seen from the system \(S’\) by this conversion.
\begin{cases} t=γ\left(t’+\frac{V}{c^2}x’ \right)\\x=γ(x’+Vt’)\\y=y’\\z=z’ \end{cases}
Be careful not to confuse both.
Why Not Conscious Lorentz Transformation in Everyday Life
The speed which we usually conscious is much slower than that of light. Cars, airplanes and even modern rockets can not even approach light speed at all. Based on this premise, we will consider why we don’t usually conscious the Lorentz transformation in everyday life.
Let \(V\) be the velocity of the system \(S’\) seen from the system \(S\) in the direction of \(x\) axis, but \(S\) is stationary. However, this speed \(V\) is sufficiently small compared with light speed \(c\). Then \(γ\) can be approximated as follows.
Substitute this into the Lorentz transformation equation.
\begin{cases} t’=t\\x’=x-Vt\\y’=y\\z’=z \end{cases}
This transformation is often seen in classical mechanics so far. Therefore, if the velocity \ (V \) is sufficiently small compared with light speed \ (c \), the effect of Lorentz transformation is negligible.
How Time Flows in a System Moving at Near Light Velocity
It is said that in a system moving at near light velocity, the flow of time will be delayed. Let’s check this with the Lorentz transformation.
Obviously \(x=Vt\), so the time \(t’\) in the system \(S’\) can now be expressed as:
Here, note that \(\sqrt{1-\frac{V^2}{c^2}}\) is always less than \(1\), then the following expression is obtained.
$$t'<t$$
Interpretation of the meaning of this expression is easy to mistake, so be careful.This expression is originally for finding the time \(t’\) of the system \(S’\) by entering the time \(t\) and the position \(x\) of the system \(S\). Therefore, the expression above means that when people in the system \(S\) compare the watches in the system \(S\) and \(S ‘\), the watch in the system \(S’\) is seen delay.
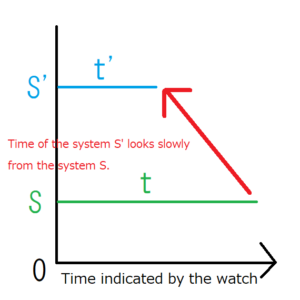
It would be easier to understand this by drawing graphs. There is a graph that indicates the time of the system \(S\) and \(S’\). Note that both the left ends is at \(0\) and \(t'<t\). By writing this graph, you can intuitively understand what the watch of system \(S’\) seems to be behind when we look at the watch of \(S’\) from system \(S\) .
Introduction of Twin Paradox
Next, what happens when you look at the watch of the system \(S\) from the system \ (S’\)? To think about this, you can use the inverse Lorentz transformation. Be careful with \(x’=-Vt’\) and transform the equation of the transformation. The reason why the right side is negative is that the system \(S\) is going in the negative direction as seen from the system \(S ‘\).
This expression shows that if you are in the system \(S’\), you can see that the watch of the system \(S\) is later than that of \(S’\).
The contradiction arises here. To summarize the above, the time of the moving system appears to flow late. The time of the system S’ appears to be late as seen from the system S and the time of the system S appears to be late as seen from the system S’. Which observation result is correct? Incidentally, this problem is famous as twin paradox.
Leave one of twins on Earth and make the other ride on a rocket that can accelerate to near the light speed. Which age is getting higher after the round-trip of the rocket? 実はThis problem can be deeply considered by using the Minkowski space and general theory of relativity. I plan to post about this later.