[mathjax]
In order to understand the centrifugal force and the centripetal force, it is first necessary to understand the imaginary force that is related with observer’s condition.
The centripetal force is the real force required for the circular movement of the object. On the other hand, the centrifugal force is the imaginary force that works when the observer moves with the object.
The direction of the centripetal force and the centrifugal force are diametrically opposed, and their magnitudes are the same. Therefore, when the observer moves with the object, it seems that the centrifugal force and the centripetal force are balanced.
The magnitude of the centripetal force or the centrifugal force \(F\) is
$$F=mrω^2=m\frac{v^{2}}{r}.$$
\(m\):mass \(r\):radius of the orbit of the object \(ω\):angular velocity[rad/s] \(v\):object speed[m/s]
Relationship between observer’s movement and imaginary force
In order to understand the imaginary force, I’ll consider how the appearance of the force changes depending on the position of the observer.
When the observer is stationary
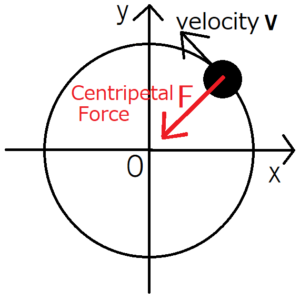
When an object is moving circularly, it can be said that the object continues to move in a tangential direction of a circular orbit. In order to maintain this circularly movement, a centripetal force toward the center of the circular orbit is exerted. The only real force related to circular movement is the centripetal force.
When the observer is moving circularly with the object
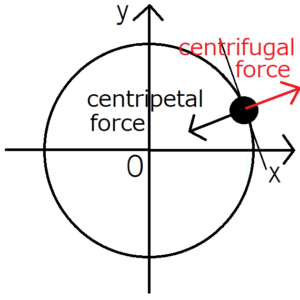
When a observer is also making a circular motion together, the observer do not notice that the object are moving circularly. However, the observer can see the real force on the object, so he or she can notice that the “force perpendicular to the direction of travel” is working. (Of course, this “force perpendicular to the direction of travel” refers to centripetal force, but since the observer does not notice the circular movement, it does not notice that this “force perpendicular to the direction of travel” is the centripetal force.)
In such a situation, since the “force perpendicular to the direction of travel” is working on the object, the observer thinks the object is going to be bent in that direction. However, the object isn’t going to be bent because it is actually in a circular movement. Based on this result, the observer thinks that there is a force that balances with the centripetal force.
This force that balances with the centripetal force is called the centrifugal force, the red arrow on the above figure. The force is called a virtual force because it does not work on the object practically as seen in the previous section.
Conclusion
· Centripetal force is the force actually working on an object.
· Centrifugal force is the virtual force which is not actually working on the object.