1. /
  2. /
  3. Method of Setting Integral Path of Complex Integral

Method of Setting Integral Path of Complex Integral

[mathjax]

I described a method of solving complex integrals by theorems before, but some complex integrals can not be solved only applying theorems. However, even with such complex integrals, it becomes possible to solve by setting an integration route yourself.

Furthermore, real integrals can be solved as complex integrals. In this article, I’ll write about some integrals that can be solved by applying this.

Set Integration Route Avoiding Singularity

If there are non-regular points within the integral route, set the route avoiding the points. Then you can easily calculate the integration you want to calculate from Cauchy’s integral theorem (if the integral route and its interior are all regular, the value of complex integral is 0). If you do not know it, I recommend reading the article below firstly.

Link:How to Solve Complex Integration by Theorems

Practice Integral \(sin/x\)

$$\int_0^∞ \frac{sinx}{x} dx$$

Transformation of the integrand

Modify \(sinx\) using the Euler’s formula.

$$\frac{sinx}{x}=\frac{e^{ix}-e^{-ix}}{2ix}$$

You should integrate only \(\frac{e^{ix}}{x}\) to calculate the integral of \(\frac{sinx}{x}\).

Since this integrand \(\frac{e^{ix}}{x}\) seems to be unable to be integrated as an elementary function, we will solve this as a complex integral. Variables of complex numbers is denoted by not \(x\) but \(z \). Therefore, if there is an imaginary part in the integral path, we express the integrand as \(\frac{e^{iz}}{z}\) from now on.

Setting the Integral Route

To avoid that the denominator of the integrand is \(0\), you must set the integral route which never contain the point of \(z=0\).

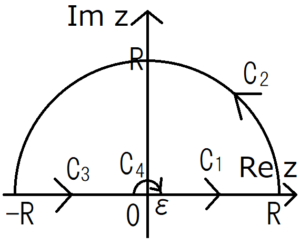
Look at the above figure. The integral route and its inside don’t contain the singularity of the integrand. The reason for being looped the integration route is for using the Cauchy’s integral theorem.

First let \(R\) be a finite value for convenience of the calculation, but eventually let it diverge to \(∞\). Likewise, \ (ε \) will eventually approach \ (0 \).

Applying Cauchy’s Integral Theorem

There are not any singularity points on the integration route \(C_1 + C_2 + C_3 + C_4\) and in its inside. Therefore the following expression holds because of the Cauchy integral theorem.

$$\int_{C_1} \frac{e^{iz}}{z} dz+\int_{C_2} \frac{e^{iz}}{z} dz+\int_{C_3} \frac{e^{iz}}{z} dz+\int_{C_4} \frac{e^{iz}}{z} dz=0$$

We will calculate each of the integral on the left side.

Integration Route \(C_1\)

$$\int_{C_1} \frac{e^{iz}}{z} dz=\int_ε^R \frac{e^{ix}}{x} dx$$

From the figure of the integration route above, the integration \(C_1\) can be expressed as follows.

$$\int_{C_1} \frac{e^{iz}}{z} dz=\int_ε^R \frac{e^{ix}}{x} dx$$

Integration Route \(C_2\)

The shape of the integration route \(C_2\) is like a semicircle, so it seems to be easier to consider using polar coordinates than using rectangular coordinates. Note that the range of the integration becomes from \(0\) to \(π\) because the standard of the angular in polar coordinates is the \(x\) axis and the more an axis rotate counter-clockwise the angular increases.

\begin{eqnarray} \int_{C_2} \frac{e^{iz}}{z} dz&=&\int_0^π \frac{e^{iRe^{iθ}}}{Re^{iθ}} \frac{dz}{dθ}dθ\\&=&\int_0^π \frac{e^{iR(cosθ+isinθ)}}{Re^{iθ}} R･ie^{iθ}dθ\\&=&\int_0^π ie^{iR(cosθ+isinθ)} dθ \end{eqnarray}

Take the absolute value of this integration.

\begin{eqnarray} \left| \int_{C_2} \frac{e^{iz}}{z} dz \right| &=& \left| \int_0^π ie^{iR(cosθ+isinθ)} dθ \right|\\&≤& \int_0^π \left| ie^{iR(cosθ+isinθ)}\right| dθ\\ &=&\int_0^π |i|･|e^{iRcosθ}|･|e^{i^2Rsinθ}|dθ\\ &=&\int_0^π 1･1･e^{-Rsinθ}dθ\\&=& \int_0^π e^{-Rsinθ}dθ\\&=& \int_0^{π/2} e^{-Rsinθ}dθ+\int_{π/2}^π e^{-Rsinθ}dθ\\&=&2\int_0^{π/2} e^{-Rsinθ}dθ \end{eqnarray}

Let’s recall the triangle inequality if you can’t understand the meaning of the inequalities above.

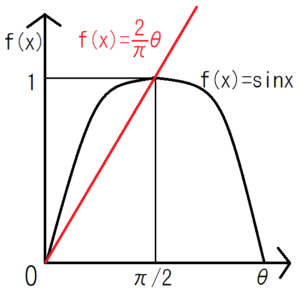
From this figure, the equation \(\frac{2}{π}<sinx\) holds in the range of \(0<θ<\frac{π}{2}\). Use this to further transform the integral.

\begin{eqnarray} \left| \int_{C_2} \frac{e^{iz}}{z} dz \right| &=&2\int_0^{π/2} e^{-Rsinθ}dθ\\&≤&2\int_0^{π/2} e^{-R･\frac{2}{π}θ}dθ\\&=&2･\left[ -\frac{π}{2R}e^{-R･\frac{2}{π}θ} \right]_0^{π/2}\\&=&\frac{π}{R} \left( 1-e^{-R} \right)\\&→&0 \quad (R→∞) \end{eqnarray}

Therefore, if \(R→∞\), the integration of the route \ (C_2 \) becomes \ (0 \).

$$\int_{C_2} \frac{e^{iz}}{z} dz→0 \quad (R→∞)$$

(Jordan’s lemma)

Integration Route \(C_3\)

Consider the integration of \ (C_3 \). It is almost the same as that of \(C_1\), but pay attention to its sign. By putting \(x=-t\), we can convert the integration.

\begin{eqnarray}\int_{C_3} \frac{e^{iz}}{z} dz&=&\int_{-R}^{-ε} \frac{e^{ix}}{x} dx\\&=&\int_{R}^{ε} \frac{e^{-it}}{-t} (-dt)\\&=&\int_{R}^{ε} \frac{e^{-it}}{t} dt\\&=&-\int_{ε}^{R} \frac{e^{-it}}{t} dt \end{eqnarray}

Since any letters can be used as variables, you can change \(t\) to \(x\) in the above expression.

$$\int_{C_3} \frac{e^{iz}}{z} dz=-\int_{ε}^{R} \frac{e^{-ix}}{x} dx$$

Integration Route \(C_4\)

\begin{eqnarray} \frac{e^{iz}}{z}&=&\frac{1}{z} \left( 1+iz+\frac{(iz)^2}{2!}+… \right) \\&=&\frac{1}{z}+\frac{1}{z}\left( iz+\frac{(iz)^2}{2!}+… \right) \\&=&\frac{1}{z}+g(z) \end{eqnarray}

It is similar to the case of \ (C _ 2 \), but be careful that the radius is \ (ε \). Paying attention to the direction of the integration, we see that the range of the integration is from \ (π \) to \ (0 \).

\begin{eqnarray} \int_{C_4} \frac{1}{z} dz&=&\int_π^0 \frac{1}{εe^{iθ}} \frac{dz}{dθ}dθ \\&=&\int_π^0 \frac{1}{εe^{iθ}} ε･ie^{iθ}dθ\\&=&-i\int_0^π dθ\\&=&-i\left[ θ\right]_0^π\\&=&-iπ\end{eqnarray}

Next consider the integral of \(g(z)\). Unlike \(\frac{1}{z}\), \(g(z)\) is regular at all points. Therefore, if \(z\) is close to \(0\), there is a positive number \(M\) that satisfies \(|g(z)|≤M\). Therefore, we can get the below transformation.

\begin{eqnarray} \left| \int_{C_4} g(z) dz\right|&≤&\int_0^π \left| g(z) iεe^{iθ} \right| dθ\\&≤&\int_0^π Mε dθ\\&=&πMε→0 \quad (ε→+0) \end{eqnarray}

From the above, the integration of \(C_4\) is summarized as follows.

\begin{eqnarray} \int_{C_4} \frac{e^{iz}}{z} dz&=&\int_{C_4} \frac{1}{z}dz+\int_{C_4} g(z) dz\\&=&-iπ \quad (ε→+0) \end{eqnarray}

Substitution of Integration Result of Each Range of Integraiton

Substitute the integral results so far into the Cauchy’s integral theorem.

\begin{eqnarray} 0&=&\int_{C_1} \frac{e^{iz}}{z} dz+\int_{C_2} \frac{e^{iz}}{z} dz+\int_{C_3} \frac{e^{iz}}{z} dz+\int_{C_4} \frac{e^{iz}}{z} dz\\&=&\int_ε^R \frac{e^{ix}}{x} dx+0-\int_{ε}^{R} \frac{e^{-ix}}{x} dt-iπ\\&=&\int_ε^R \frac{e^{ix}-e^{-ix}}{x} dx-iπ\\&=&2i\int_ε^R \frac{e^{ix}-e^{-ix}}{2ix} dx-iπ\\&=&2i\int_ε^R \frac{sinx}{x} dx-iπ\end{eqnarray}

Take the limit of \(ε \to 0\), \(R \to ∞\), and the final answer comes out.

$$\int_0^∞ \frac{sinx}{x} dx=\frac{π}{2}$$

Leave a Reply

*

CAPTCHA