1. /
  2. /
  3. Fourier Transform

Fourier Transform

[mathjax]

I thought about Fourier series expansion before, but this time it is an introduction of Fourier transform.

Fourier transform

$$F(k)=\int_{-∞}^{∞} f(x)e^{-ikx} dx$$

inverse Fourier transform

$$f(x)=\frac{1}{2π}\int_{-∞}^{∞} F(k)e^{ikx} dk$$

Suppose a wave is given by the function \(f(x)\). Using Fourier transform, the function of wave \(f (x)\) is expressed as a function \(F(k)\) of wavenumber \(k\). \(F(k)\) is the function which decomposes \(f(x)\) into the sine waves of all wavenumbers \(k\) and expresses the size of each the sine wave as a function. You can convert the wave \(f (x)\) to \(F(k)\) by Fourier transform and \ (F (k) \) to \(F(k)\) by inverse Fourier transform.

How to Memorize the Formula

The Fourier transform is to remove the variable \(x\) from \(f (x)\) and find \(F(k)\). So, in the Fourier transform formulas, \(f(x)\) is integrated by \(dx\).

We consider the inverse Fourier transform as well. This is a conversion to find out \(f (x)\) by kicking out the variable \(k\) from the function \(F(k)\). Therefore, in the inverse Fourier transform formulas, \(F(k)\) is integrated by \(dk\).

Difference between Fourier series expansion and Fourier transform

Periodic or NOT Periodic

The Fourier series expansion can be used only when \(f(x)\) is a periodic function. On the other hand, the Fourier transform can be used not only when \(f(x)\) is a periodic function, but also when it is not. As you can see from the formula above, the Fourier transform formula does not include the period \(L\) unlike the Fourier series expansion formula.

continuous and discrete spectrum

Fourier series expansion expresses the wave \(f(x)\) by superposition of sine waves.

On the other hand, if you use Fourier transform, you can find the wavenumbers of sine wave contained in \(f (x)\) by finding \(F(k)\).

If \ (F (k) \) is continuous, it is called continuous spectrum. Then if \ (F (k) \) is discrete, it is called a discrete spectrum.

Practice

Fourier transform the following function

$$\begin{eqnarray} f(x)=\begin{cases} 1 & (-2<x<5)  \\ 0 & (x<-2,5<x) \end{cases} \end{eqnarray}$$
$$\begin{eqnarray} F(k)&=&\int_{-∞}^{∞} f(x)e^{-ikx} dx \\ &=&\int_{-∞}^{-2} 0･e^{-ikx} dx+\int_{-2}^{5} 1･e^{-ikx} dx+\int_{5}^{∞} 0･e^{-ikx} dx \\ &=&0+\left[ -\frac{1}{ik}e^{-ikx} \right]_{-2}^{5}+0 \\ &=& -\frac{i}{i^{2}k}(e^{-i･5k}-e^{+i･2k}) \\ &=&\frac{i}{k}\left[ cos(+5k)-isin(+5k)-\{cos(2k)+isin(2k)\}\right] \\ &=&\frac{i}{k}\left[ cos(5k)-cos(2k)-i\{sin(5k)+sin(2k)\}\right] \\ &=&\frac{1}{k}\left[ sin(5k)+sin(2k)+i\{cos(5k)-cos(2k)\}\right] \end{eqnarray}$$

Here we used the Euler formula for the transformation of lines 4 to 5.

When the White Light of the Television Is Fourier Transformed

According to the article about the Fourier series expansion that I wrote before, when the periodic white light of television is expanded Fourier series, waves representing the three primary colors of light are obtained. Then, what if we convert with Fourier instead?

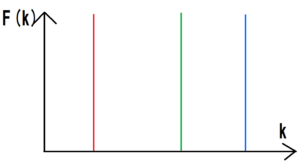
If the white light is Fourier transformed, we will get the above figure. As shown in the figure, a large peak is formed only at the wavenumbers representing red, blue, and green, but in other regions there will be no peaks.

The longer the wavelength, the smaller the wavenumber becomes. Therefore, the wavenumber of red light is smaller than that of other kinds of light.
Similarly, the shorter the wavelength, the bigger the wavenumber becomes, so the wavenumber of blue light is bigger than that of other kinds of light.

Leave a Reply

*

CAPTCHA