[mathjax]
On 20th November 2017, NTT announced a system using domestic quantum computer for general people. Recently we often hear about quantum computers, but what is the difference between such computers and ordinary computers?
In this article, I will briefly touch on the difference between quantum computer and conventional computer, and a quantum dot used for quantum computer.
What is Conventional Computers?
Before writinging about a quantum computer, I will first describe an ordinary computer.
A normal computer is running with only two kinds of signals “0” and “1”. If you have used the Internet a lot, I think you’ve heard that at least once. In general, “0” means a low potential level, “1” means a high potential level. The method of calculating using these two types of symbols is called the binary system.
Difference between Quantum Computer and Conventional Computer
A conventional computer calculates using “0” and “1” as a minimum unit, whereas a quantum computer calculates using a quantum memory as a minimum unit. This quantum memory contains several quantum dots (quantum bits).
The decisive difference between the potential levels and the quantum memories is that the number of states that can be expressed in one minimum unit is different. Specifically, when we use the potential levels, only two kinds of states “0” and “1” can be expressed. On the other hand, one quantum memory can express \(2^n\) kinds of states.
Why Quantum Memory Can Represent Many States
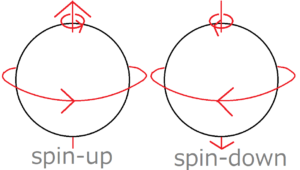
The identity of a quantum dot is a very small particle. The identity of a quantum dot is a very small particle like an electron. In order to put information on electrons, we need to assign two states of electrons to “0” and “1” respectively. For example, if you want to assign the states of electron spin to “0” and “1”, you can assign them to the state of “spin-down” and “spin-up” respectively.
What is electronic spin?
Electrons rotate like the Earth. Then depending on the direction of rotation, it is said to be “spin-down” or “spin-up.” This direction of spin corresponds to the direction of the right-hand thread.
Electrons Are Not Only Particles But Wave
Small objects such as electrons have both particle and wave properties. That means the state of electrons can be represented by the principle of superposition like that of waves. Therefore, even spins of electrons can be represented by superimposition. Given the superposition of spins, electrons can rotate clockwise and also rotate counterclockwise at the same time. The common sense of the world of the quantum level is much different from that of our world.
By the way, when you observe the electron of the superposition state, the superposition is broken. Then the electron come to rotate either clockwise or counterclockwise.
The superposition of the electron spin can be expressed using mathematical expressions as follows.
If you have studied quantum mechanics, you may be more familiar with the below equation.
The first term on the right side refers to the state of spin-down and the second term refers to a state of spin-up.
If neither of the two constants \(α\) nor \(β\) are \(0\) in the above equation, neither of the vector components \(a_1\) nor \(a_2\) are also \(0\). Then the state neither components \(a_1\) nor \(a_2\) of the vector are not \(0\) indicates that the electron rotate clockwise and also counterclockwise at the same time.
Why Quantum Memories Can Represent Many States
The key word of the reason quantum memory can express many states is the superposition of electronic states. In the above formula, \(α\) and \(β\) can be obtained at the same time if \(|a>\) can be detected.
One Quantum Dot in One Quantum Memory
For example, assume an electron with the spin is observed like below.
Substituting this expression into the left side of the vector equation, the spin of the observed electron is a superposition of spin-down \(0\) and spin-up spin \(1\).
From the above work, we could observe the state of two kinds of electrons “downward spin” and “upward spin” by only observing one electron.
When Quantum Dots in One Quantum Memory Are Increased
Let’s review the probability here. When you throw a coin \(n\) times, the number of possibility is \(2^n\).
Given this fact, let’s consider the case where two quantum dots are observed. Observing two quantum dots, we can obtain its number of possibility: \(2^2=4\). Similarly, Observing \(n\) quantum dots, we can obtain its number of possibility: \(2^n\). That’s why I mentioned one quantum memory can represent the state of \(2^n\) streets.
Quantum computers can simultaneously calculate a large number of mathematical expressions using superposition of this states.
Benefit of Quantum Computers
What is the advantage of using quantum dots? Actually, there are many calculations which conventional computers aren’t good at calculating. For example, it is said that it takes 10 years to calculate factorization of 200 digits with a conventional computer. Then 10,000 digits of factorization will reach 100 billion years. However, if you use a quantum computer, factorization of 200 digits ends in several minutes. In addition, even factorization of 10,000 digits ends in few hours or days.
In other words, the advantage of using quantum computers is to be able to solve calculations that can not be done with conventional computers.
Conclusion
・Quantum computers calculate by using quantum memory as the minimum unit.
・Quantum computers can calculate even those which can not be calculated by conventional computers.