1. /
  2. /
  3. Laplace Transform and Algebraic Equation

Laplace Transform and Algebraic Equation

[mathjax]

Laplace transform refers to the following conversion \(F(s)\).

$$F(s)=\int_0^∞ f(t)e^{-st}dt$$

The function before Laplace transform \(f(t)\) depends on \(t\), but the function after Laplace transform \(F(s)\) depends on \(s\).

Why Use Laplace Transforms

The advantage of Laplace transform is to be able to convert differential equations into algebraic equations.

Practice1 Method of Laplace Transform

Let’s find the Laplace transform of the following function. It’s just a simple integration problem.

$$f(t)=e^{αt}$$
\begin{eqnarray} F(s)&=&\int_{0}^{∞}e^{αt}e^{-st} dt \\&=&\int_{0}^{∞} e^{(α-s)t} dt\\&=&\left[ \frac{1}{α-s}e^{(α-s)t} \right]_{0}^{∞}\\&=&\frac{1}{α-s}\left (  (\displaystyle \lim_{ t \to \infty }e^{(α-s)t}) -e^0 \right)\\&=&\frac{1}{s-α} \end{eqnarray}

However, it was calculated on the assumption that \(s-α\) is positive. Otherwise \(\displaystyle \lim_{t \to \infty} e^{(α – s)t}\) does not converge to \ (0 \).

Table of Laplace Transforms

It is troublesome to calculate Laplace transform each time, so there is a table that summarizes functions before and after Laplace transforms. It is called the table of Laplace transforms. It will be useful enough to solve the example below.

However, since this table already exists too much on the Internet, I don’t write write here. It is obtained immediately by searching.

Practice2 LR Series Circuit

Consider the current flowing in the LR series circuit as an example of differential equation. This practice was solved without using the Laplace transform in the previous article. We recommend that you also refer to the article.

Link:Characteristics of Coil, Resistor and Capacitor

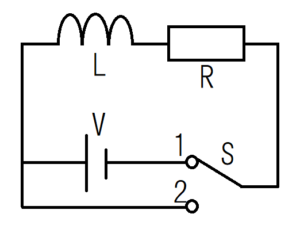
In this practice, find the current \(i(t)\) when switch 1 is turned on at time \(t=0\) with the Laplace transform. Switch 2 is not used.

First of all, on this page, the current function before Laplace transform is represented by the small letter \(i(t)\) and the current after Laplace transform is represented by the capital letter \(I(s)\). If we note that the current depends on \ (t \) before Laplace transform and \ (s \) after the transform, it will be difficult to confuse them.

Laplace Transform and Algebraic Equation

The direct current \(i(t)\) that flows in the LR series circuit is written as follows.

$$L\frac{di(t)}{dt}+Ri(t)=V$$

Transform this equation using Laplace transform table.

$$L(sI(s)-i(0))+RI(s)=\frac{V}{s}$$

Note that even the constant \(V\) is also converted to \(\frac{V}{s}\). Then as the initial condition, we consider the state that current does not flow at time \(t=0\), so we assign \(i(0)=0\).

$$LsI(s)+RI(s)=\frac{V}{s}$$

Solve this algebraic equation for \(I(s)\).

\begin{eqnarray} I(s)&=&\frac{V}{s(sL+R)} \\ &=& \frac{V}{R} \frac{1}{s(1+\frac{L}{R}s)}\end{eqnarray}

Partial fraction decomposition

Here, to facilitate fitting to the Laplace transform table, we decompose \(\frac{1}{s(1+\frac{L}{R}s)}\). Consider to decompose \(\frac{1}{s(1+\frac{L}{R}s)} \) using the constants \(A\) and \(B\).

$$\frac{1}{s(1+\frac{L}{R}s)}=A\frac{1}{s}+B\frac{1}{1+\frac{L}{R}s}$$

First, multiply both sides by \(s(1+\frac{L}{R}s)\) to cancel the denominator of the term containing \(A\) and \(B\).

$$1=A\left( 1+\frac{L}{R}s \right)+Bs$$

The above expression should hold true with any \(s\). Therefore, if you assign \(s\) such that either of the two terms on the right side disappears, the constants \ (A \) and \ (B \) are obtained.

Substitute 0 for s and the constant \ (A \) is obtained as shown below.

$$1=A \left( 1+\frac{L}{R}･0 \right)+B･0$$
$$A=1$$

Then substitute \(-\frac{R}{L}\) for \(s\) and you get the value of \(B\).

$$1=A\left(1+\frac{L}{R}･(-\frac{R}{L}) \right)+B･\left( -\frac{R}{L} \right)$$
$$B=-\frac{L}{R}$$

From the above, the partial fraction decomposition is completed.

$$\frac{1}{s(1+\frac{L}{R}s)}=\frac{1}{s}-\frac{L}{R}\frac{1}{1+\frac{L}{R}s}$$

Current after Laplace transform

Therefore, the current after the Laplace transform is obtained as follows.

\begin{eqnarray} I(s)&=&\frac{V}{R} \frac{1}{s(1+\frac{L}{R}s)}\\&=&\frac{V}{R}\left( \frac{1}{s}-\frac{L}{R}\frac{1}{1+\frac{L}{R}s} \right)\\ &=& \frac{V}{R} \left( \frac{1}{s}-\frac{1}{\frac{R}{L}+s} \right)\end{eqnarray}

Current Before Laplace Transform

Finally, convert this to the current based on the Laplace transform table.

$$i(t)=\frac{V}{R}(1-e^{-\frac{R}{L}t})$$

This result coincides with the current that is found without the Laplace transform.

Confirm that the current after Laplace transform depends on \ (s \) and the current before Laplace transform depends on time \ (t \).

Conclusion

･The Laplace transform converts differential equations into algebraic equations.

･The Laplace transform table makes calculations of Laplace transforms smoothly.

Leave a Reply

*

CAPTCHA