ほとんどの相対性理論の本は、この「ローレンツ変換」から始まる。ローレンツ変換とは、異なる動き方をしている、2つの系の時刻や空間を結びつけるような変換である。今まで学んできた力学や電磁気学などと違い、相対性理論で言っていることは、初見ではすぐには信じられないことばかりだろう。例えば、質量を持つ物体は光速に追いつけないことや、光速に近い速さで動いていると時間の進み方が遅くなることなど。この記事を読み進めることで、ローレンツ変換の意味をじっくり考えてみてほしい。
ローレンツ変換の式
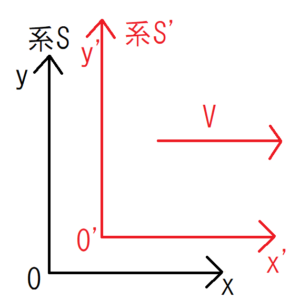
とある系\(S\)と、系\(S\)から見て\(x\)方向に速度\(V\)で動いている系\(S’\)が存在する。それぞれの系には時計が存在し、系\(S\)の時刻は\(t\)、系\(S’\)の時刻は\(t’\)だとわかる。また、それぞれの系の座標は、系\(S\)は\(x,y,z\)、系\(S’\)は\(x’,y’,z’\)で表される。
このとき、ローレンツ変換は次のように表される。
$$β=\frac{V}{c}$$
この変換によって、系\(S\)から見たときの系\(S’\)の様子がわかる。
ちなみに、ローレンツ変換を施しても値が変わらないことを、ローレンツ変換に対して共変的であるという。
ローレンツ逆変換の式
ローレンツ逆変換は、ローレンツ変換とは逆で、系\(S’\)を系\(S\)に変換するようなものである。
この変換によって、系\(S’\)から見たときの系\(S\)の様子がわかる。
両者を混同しないように注意すること。
例題 普段の生活でローレンツ変換を意識しない理由
普段我々が意識している速さというものは、光速と比べてはるかに遅いものである。ボルトも車も飛行機も現代のロケットですらも、光速に近づくことすらできない。この前提を基に、なぜ普段はローレンツ変換を意識しないのか考える。
静止している系を\(S\)、\(x\)方向に速度\(V\)で動いている系を\(S’\)とする。ただし、この速度\(V\)は、光速\(c\)と比べて十分小さい。すると、\(γ\)は次のように近似できる。
これをローレンツ変換の式に代入する。
\begin{cases} t’=t\\x’=x-Vt\\y’=y\\z’=z \end{cases}
この変換は、今までの古典力学でもよく見てきた、ただの\(x\)方向に速度\(V\)で動く系\(S’\)の変換である。よって、速度\(V\)が光速\(c\)と比べて十分小さい場合、ローレンツ変換の影響は無視できる。
例題 光速に近い速度で運動している系での時間の流れ方
光速に近い速さで動いている系では、時間の流れが遅くなるといわれている。このことをローレンツ変換を使って確かめる。
(距離)=(速さ)×(時間)より、\(x=Vt\)である。これで、系\(S’\)の時刻\(t’\)は次のように表せる。
ここで、\(\sqrt{1-\frac{V^2}{c^2}}\)は常に\(1\)より小さいことに注意すると、次の式が得られる。
$$t'<t$$
この式の意味の解釈は間違えやすいから気を付ける。この式は元々、系\(S\)の時間\(t\)と位置\(x\)を入力することで、系\(S’\)の時間\(t’\)を求める式であった。だから、上の式は、系\(S\)の人が、系\(S\)と\(S’\)の時計を比べると、系\(S’\)の時計の方が遅れているように見えるという意味となる。
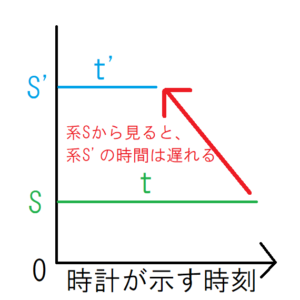
このことは実際にグラフにした方が直感的にわかりやすいだろう。今、2つの系\(S\),\(S’\)にそれぞれ時計を設置して、その両方とも\(0\)を指した時刻を左端にそろえたグラフを書く。\(t'<t\)を考慮すると、上の図が描ける。この図を書くことで、系\(S\)から系\(S’\)の時計を見ると、系\(S’\)の時計が遅れているように見えることが直感的に理解できる。
では、これまでとは逆で、系\(S’\)から系\(S\)の時計を見たときはどうなるだろう。これについて考えるには、ローレンツ逆変換の式を、先ほどと同じように変形すればよい。\(x’=-Vt’\)に気を付けて変形する。右辺にマイナスがついている理由は、系\(S’\)から見たら、系\(S\)は負の方向へ進んでいるように見えるからである。
この式は、系\(S’\)の人が、系\(S\)と\(S’\)の時計を比べると、系\(S\)の時計の方が遅れているように見えるという意味となる。
ここで矛盾が生じる。上のことをまとめると、運動している系の時間は遅く流れているように見えるということになる。系\(S\)にいる人にとっては系\(S’\)の時間は遅れて見えるし、系\(S’\)にいる人にとっては系\(S\)の時間は遅れて見える。どちらの観測結果が正しいのだろうか。ちなみに、この問題は有名で、双子のパラドックスと呼ばれている。同い年である双子の片方を地球に残し、もう片方は光速付近まで加速できるロケットに乗せる。ロケットが往復してきたとき、どちらの年齢が高くなっているか、という問題だ。実はこの問題は、ミンコフスキー空間というものを用いると深く考察できる。これについては後日記事にする予定である。
追記:2018/02/03
双子のパラドックスの記事を書きました。
参考文献
・竹内淳(2013)『高校数学でわかる相対性理論』,講談社.

