
トンネル効果というものを聞いたことがあるだろうか。ざっくり説明すると、物体が通常では通り抜けできない壁を通り抜けてしまう現象のことである。
このトンネル効果は、素粒子のような極めて小さい物体ならよく起こるものだが、通常人間が意識するようなレベルの大きさでは全くといってもいいほど起こらない。
この記事では、実際に人間が壁を通り抜けられる確率を具体的に計算して、それがいかに非現実的であるかを解説する。
粒子としての性質と波としての性質
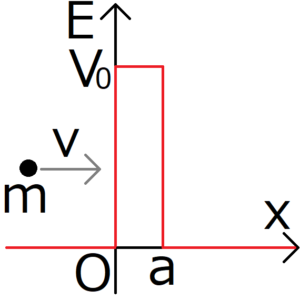
上の図は、粒子を壁に飛ばしている様子を表す。赤い線の出っ張りが壁を表している。
運動しているあらゆる物体は、粒子としての性質と共に、波としての性質を併せ持つ。したがって、粒子を壁に飛ばすという行為は、波をポテンシャルに入射させる行為に置き換えができる。
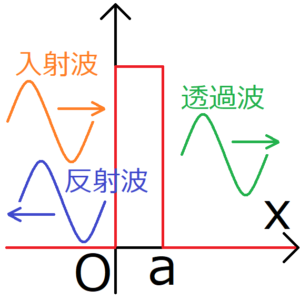
この波の絶対値の2乗は、粒子の存在する確率(存在確率)という物理的意味を持つ。波があるところに粒子が存在しうると言ってもいい。
波をポテンシャルに入射させると、その波はポテンシャルに反射されるものと、ポテンシャルを通過するものに分けられる。反射された波を反射波、通過するものを透過波と呼ぶ。
つまり、透過波が存在するということは、粒子がポテンシャルを通り抜ける可能性があるということになる。
反射率と透過率
反射率とは、入射される粒子の存在確率がポテンシャルによって反射される確率のことである。ポテンシャルに飛ばした粒子が反射される確率ともいえる。
一方透過率とは、存在確率がポテンシャルを透過する確率のことである。飛ばした粒子がポテンシャルを透過する確率ともいえる。つまり、この透過率こそが、トンネル効果で人が壁をすり抜けられる確率のことを指す。
ポテンシャルの幅\(a\)を使って反射率\(R\)と透過率\(T\)を数式で表すと、次のようになる。
ここで、\(k\)と\(κ\)はそれぞれ次のように定義される。
\(V_0\)はポテンシャルの大きさ、\(E\)は粒子のエネルギー、\(m\)は粒子の質量、\(ħ\)はディラック定数と呼ばれるものである。
透過率と反射率の和は、必ず1になる。
人が壁をすり抜けられる確率
ここまで読み飛ばした方のためにもう一度説明するが、人が壁をすり抜けられる確率\(T\)とは次の数式で与えられる。
この式中の変数の意味は少し前に書いてあるが、別にほとんどわからなくても問題ない。ただし、\(m\)が粒子の質量、\(a\)が壁(ポテンシャル)の幅だということだけは覚えておこう。
上の確率\(T\)はかなり複雑に見えるが、実は粒子のエネルギー\(E\)がポテンシャル\(V_0\)よりも十分小さいとき、下のように近似できることが知られている。
では、この近似を使って、実際に人が壁をすり抜けられる確率を求める。
今回考える壁
今回は、体重50.0kgの人が時速5.00km(秒速1.39m)で、高さ2.00mで厚さ15.0cm(0.150m)の壁に突っ込んだ場合の、人が壁をすり抜ける確率\(T\)を求める。
上の\(T\)の近似式の変数にこの仮定を当てはめると、次のようになる。
ポテンシャル\(V_0\)は高校物理で学習した位置エネルギーである。
これらを上の近似式に代入すればよい。
残念ながら、管理人には\(e^{-10^{33}}\)を計算できるツールを見つけられなかったため、これをネイピア数\(e\)を使わずに求めることはできなかった。
エクセルにでも入力してみればわかるが、これを計算しようとしても結果が0と表示されてしまうため、この確率は厳密には計算できないようである。
参考までに、
らしいので、\(e^{-10^{33}}\)も相当小さいと思われる。
おまけ
ちなみに、地球に生命が生まれる確率は
程度らしいので、人が壁を通り抜ける確率は、この確率よりも比較することすら憚られるレベルで小さいことがわかる。
まとめ
トンネル効果を人間のスケールで実験するのはあきらめたほうがいいだろう。
最後に
透過率と反射率の導出については、下の記事を参照してください。こちらではシュレディンガー方程式を使って、波動関数を求めたり透過率と反射率を求めたりしています。
参考文献
・村上雅人(2006)『なるほど量子力学〈2〉』,海鳴社.
・CASIO,”高精度な高等関数が使えるフリー計算”(https://keisan.casio.jp/calculator).
・冒頭の写真の出典『写真AC』(https://www.photo-ac.com/)


