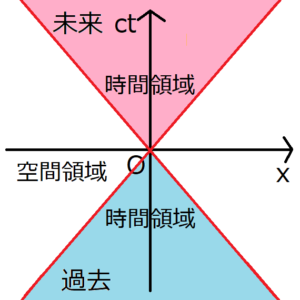
ミンコフスキー空間とは、横軸に場所、縦軸に時間をとり、原点に観測者を置いた空間のことである。ミンコフスキー空間上の直線の傾きは、物体の速度を表す。特に、縦軸を\(ct\)でとっているため、光速の傾きが45度になる。この光速を表す線を母線とする円錐を、光錐と呼ぶ。
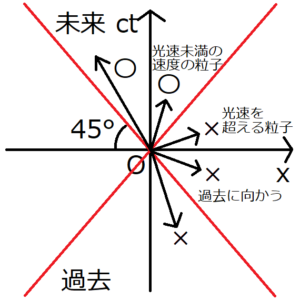
あらゆる物体は光よりも早く動けないので、ミンコフスキー空間上で物体の運動を考えるとき、その物体を表す矢印の傾きは赤い線より大きくなくてはならない(矢印は光錐の内部にのみ存在できると言い換え可能)。さらに、物体は過去には進まないため、物体を表す矢印は下方向には向かない。
ミンコフスキー空間の分割
ミンコフスキー空間は、光速を表す線によって3種類に分割される。それぞれ何を表しているかを考える。
時間領域
分割された部分のうち、時間軸ctを含む領域を時間領域と呼ぶ。
未来を表す部分
上の図で赤く塗られている部分は、原点の人から見て未来を表している。
過去を表す部分
上の図で青く塗られている部分は、原点の人から見て過去を表している。
空間領域
上の図で白くなっている部分は、空間領域と呼ばれる。
光速度不変とミンコフスキー空間
静止系\(S\)と運動系\(S’\)で、ミンコフスキー空間の軸がどのように変わるのか見ていこう。具体的な方法として、ローレンツ逆変換を使って、系\(S’\)上の座標\((ct’,x’)=(0,1),(1,0)\)は、系\(S\)上ではどの座標に対応するか考える。
静止系\(S\)に対して系\(S’\)がx軸方向に速度\(V\)で動いているとすると、ローレンツ逆変換は、次のような式となる。(\(β=V/c, γ=1/\sqrt{1-β^2}\))
参考:ローレンツ変換の意味
今、系\(S’\)の速度\(V\)は\(V=0.80c\)とする(つまり光速の80%の速度)。ローレンツ変換\((ct’,x’)=(0,1)\)も代入すると、
同様に\((ct’,x’)=(1,0)\)も代入する。
以上の情報を踏まえて、同じミンコフスキー空間上に系\(S,S’\)の軸を描いてみる。
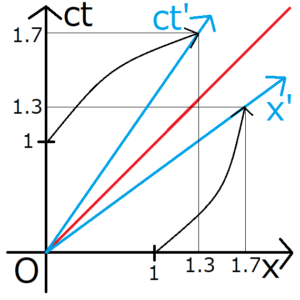
光速を表す線を赤線、静止系\(S\)の軸を黒線、運動系\(S’\)の軸を水色の線で表した。
ここまでの考察より、静止系\(S\)の座標における座標(x,ct)=(1,0)と座標(x,ct)=(0,1)は、運動系ではそれぞれ(x,ct)=(1.7,1.3)と(x,ct)=(1.3,1.7)に変換されることがわかった。運動系の軸はこれらの点と原点を通るため、そのような水色の線を引けば、運動系\(S’\)の軸が求まる。
この図から、運動している系\(S’\)の座標軸は、光を表す赤線に近づくことがわかる。
参考文献
・平川浩正(1986)「相対論」,共立出版株式会社.
・二間瀬敏史(2005)『よくわかる相対性理論』,ナツメ社.