1. /
  2. /
  3. ローレンツ収縮とその導出

ローレンツ収縮とその導出

  • このエントリーをはてなブックマークに追加
  • LINEで送る

静止している系から光速近くで動いている物体を観察する。すると、その物体は本来の長さ(物体が停止しているときの長さ)よりも短く見える。この現象のことをローレンツ収縮とよぶ。

物体が停止しているときの棒の長さを\(L_0\)、物体が動いている様子を静止系から見たときの棒の長さを\(L\)とすると、両者の間には次の関係が成り立つ。ただし、運動系S’は、系Sに対してx方向に速度Vの速さで動いていて、かつ棒は系S’と同じように動いているものとする。

\begin{eqnarray} L&=&L_0\sqrt{1-\frac{V^2}{c^2}}\\&=&L_0\sqrt{1-β^2} \end{eqnarray}

ローレンツ収縮の導出

ローレンツ変換の復習

\begin{cases} t’=γ\left(t-\frac{V}{c^2}x \right)\\x’=γ(x-Vt)\\y’=y\\z’=z \end{cases}
$$γ=\frac{1}{\sqrt{1-\frac{V^2}{c^2}}}=\frac{1}{\sqrt{1-β^2}}$$

$$β=\frac{V}{c}$$
参考:ローレンツ変換の意味

ローレンツ収縮の導出

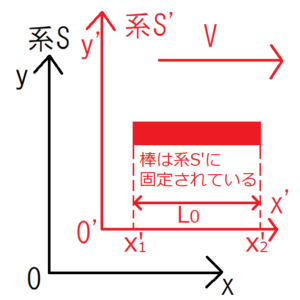
静止系\(S\)に対して、運動系\(S’\)がx軸方向に速度\(V\)で動いている。さらに、長さ\(L_0\)の棒が運動系\(S’\)と同様に動いているとする。

系\(S\)から見た棒の片方の先端の位置を\(x_1\)、もう片方の先端の位置を\(x_2\)とする。同様に、系\(S’\)から見た棒の片方の先端の位置を\(x’_1\)、もう片方の先端の位置を\(x’_2\)とする。棒は系\(S’\)と同じように動いているため、この棒は系\(S’\)で観察すると静止しているように見える。そのため、系\(S’\)上で観察したときの棒の長さ\(x’_2-x’_1\)は元の棒の長さ\(L_0\)となる。

$$x’_2-x’_1=L_0$$

ではこれから、静止系\(S\)から棒を観察したときの棒の長さ\(L\)を、\(L_0\)を使って表現する。

まずローレンツ変換より、\(x_1\)と\(x’_1\)、\(x_2\)と\(x’_2\)の関係はそれぞれ次のようになる。

\begin{eqnarray}  \left\{ \begin{array}{l} x’_1=γ(x_1-Vt) \\ x’_2=γ(x_2-Vt) \end{array} \right. \end{eqnarray}

後は\(L_0=x’_2-x’_1\)に上のローレンツ変換を代入すればよい。

\begin{eqnarray} L_0&=&x’_2-x’_1\\&=&(γ(x_2-Vt))-(γ(x_1-Vt))\\&=&γ(x_2-x_1)\\&=&γL \end{eqnarray}

両辺を\(γ\)で割ると、

$$L=L_0\sqrt{1-\frac{V^2}{c^2}}$$

ここで、\(\sqrt{1-\frac{V^2}{c^2}}<1\)だから、

$$L_0>L$$

この式から、静止している系\(S\)から観測される棒の長さ\(L\)は、棒の元の長さ\(L_0\)よりも短くなる。

まとめ

運動している棒を静止している系から観察すると、進行方向に縮んで見える。

参考文献

・戸田盛和(1997)『物理学30講シリーズ7 相対性理論30講』,朝倉書店.

  • このエントリーをはてなブックマークに追加
  • LINEで送る

SNSでもご購読できます。

コメントを残す

*

CAPTCHA