双子のパラドックスの解き方

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

前の記事では、静止している系から運動している系の時計を見ると、時刻が遅れて見えることを確認した。

ところが、運動系から見ると静止系は動いて見えるため、運動系からも静止系の時計は遅れて見えるはずである。これでは、互いに相手の時計が遅れて見えることになり、矛盾が生じる。

この問題は、地球にいる双子の弟と光速に近い速度のロケットに乗っている兄が再開したとき、どちらが年上か、という問題に置き換えられる。これを、双子のパラドックスという。この記事では、ミンコフスキー空間を使って双子のパラドクスを解いてみる。

1 前提知識
- 1.1 ミンコフスキー空間とは
- 1.2 世界間隔と固有時
2 双子のパラドクスの解法
3 加速度運動と時間の遅れ
4 まとめ
5 参考文献

前提知識

ミンコフスキー空間とは

ミンコフスキー空間とは、縦軸を時間$ct$、横軸に位置$x$をとった空間のことである。

参考:ミンコフスキー空間とは

世界間隔と固有時

世界間隔とは、ミンコフスキー空間上の2点間の距離のことである。これはローレンツ変換で変化しないため、慣性形によらない。

$$(Δs)^2=-c^2(t_1-t_2)^2+({\bf r}_1-{\bf r}_2)^2$$

また、固有時$Δτ$は次のように定義された。

$$Δτ=\frac{\sqrt{-ds^2}}{c}=\sqrt{1-\left( \frac{v}{c} \right)^2 }dt$$

参考:世界間隔の共変性と固有時について

双子のパラドクスの解法

双子の兄をロケットに乗せて、弟を地上に残す。このロケットは地球から16光年離れた星まで往復する。ロケットは光速の64%の速さで動くとする。

結論から言うと、地上で二人が再開したとき、地上にいた弟のほうが年をとった状態になる。兄から見たら未来にタイムスリップしたような感じだろう。今からそうなる理由を説明する。

ミンコフスキー空間上のロケットの軌跡

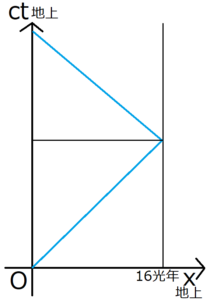
上のミンコフスキー空間の軸はどちらも地上が基準となっている。青線は、ミンコフスキー空間上におけるロケットの軌跡を表す。

世界間隔の求め方

往路の世界間隔が求まれば、それをもとにロケットから見た星に到着した時間と固有時が求まる。この固有時から、地上とロケットの時間の差が求まる。

ロケットは光速の64%で16光年先の星に向かっているため、静止系から見たときの到着する時間は、次のように予想される。

$$16×\frac{1}{0.64}=25[年]$$

往路の世界間隔は、次のようになる。

$$(Δs)^2=-25^2+16^2=-12^2$$

普段使っている三平方の定理とは違い、時間の項の符号が負になっているので注意。

ロケットから見た星への到着時間

次に、ロケットから見たときの、星に到着した時間を考える。

ロケットの運動系でも世界間隔は同じく、$(Δs)^2=-12^2$である。兄から見たらロケットは静止系だから、$dx=0$だ。これらを世界間隔の式に代入する。

$$-12^2=-(ct)^2+0^2$$

$$ct=12[年]$$

以上から、ロケット内の時計で12年後に、星に到着することがわかる。

固有時の求め方

ロケットにおける到着時間が求まったため、固有時$τ$が求められる。光速を$c$としたときのロケットの速さは$0.64c$となることを思い出す。

\begin{eqnarray} τ&=&t\sqrt{1-\left( \frac{v}{c} \right)^2 }\\&=&12×\sqrt{1-\left( \frac{0.64c}{c} \right)^2 }\\&≒&9.2[年] \end{eqnarray}

地上から見た到着までの時間

弟は地上から動かないため、固有時の方程式に$v=0$を代入する。

$$9.2=t\sqrt{1-\left( \frac{0}{c} \right) }$$

$$t=9.2[年]$$

よって、兄が12年かけて星に到着したとき、地上では9.2年しか経過していない。

復路も同様にして考えると、兄が星を出発したときの地上は、地上を出発したときから40.8年経過しているといえる。

折り返しただけで32年経過する

では、今までのことをミンコフスキー空間上にまとめてみよう。

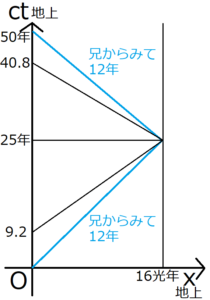
この図から、地上の時計で出発直後から9.2年までの間で兄は星に向かい、40.8年から50年までで地上に向かうことがわかる。では、9.2年から40.8年までの31.6年間、兄はどういう状態なのだろうか。

この間、兄は星に到達し、地上に向かうために折り返している。つまりこの計算結果は、兄が地上へ方向転換した瞬間に、地上で31.6年経過することを表している。

加速度運動と時間の遅れ

一般相対性理論によると、重力によって時間の遅れが生じるとされている。そして加速度運動に伴って発生する見かけ上の力は、重力と同じ性質を持っている。したがって、加速度運動は時間の遅れを生み出す。

ロケットの方向転換も加速度運動である。光速と比較できるくらい速い速度から減速して停止し、そこから地球に向けて再び加速する。この加速度運動の過程でロケット内の時間の進みが遅れるため、折り返しが終わるときには地球で何十年も経過している。

参考:円運動から学ぶ見かけ上の力

まとめ

・光速に近いロケットに乗った兄と地上の弟の年齢を比べたら、最終的には兄の年齢のほうが若くなる。

・一般相対性理論より、ロケットの折り返しで地上の時間が何十年も経過することがある。

これを読んだ後だと、新幹線や飛行機も極々近い未来に行けるタイムマシンだということもすんなり納得がいくだろう。乗り物に乗るたびにこんなことを意識する人はほとんどいないだろうが。

参考文献

・二間瀬敏史(2005)『よくわかる相対性理論』,ナツメ社.

・竹内淳(2013)『高校数学でわかる相対性理論』,講談社.

双子のパラドックスの解き方