[mathjax]
デルタ関数δ(x−a)とは、カッコの中が0のときのみ特殊な値になるようなものであり、次のようにして定義される。
∫∞−∞f(x)δ(x−a)dx=f(a)
このデルタ関数は名前に関数とついているが、正確には関数ではない。そのため、このように積分を使って定義される。
デルタ関数について
デルタ関数には、次の2つの性質がある。
1.デルタ関数δ(x−a)を、xの値で場合分けすると、次のようになる。
δ(x−a)={∞(x=a)0(x≠a)
つまり、デルタ関数をグラフ化すると、次のようになる。
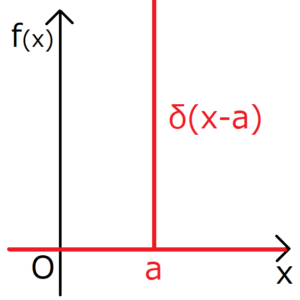
2.デルタ関数を全空間で積分した値は1になる。
∫∞−∞δ(x−a)dx=1
ただし、x=a以外の場所ではデルタ関数は0になるため、「δ(x−a)を、x=aを含む範囲で積分した値は1になる」と言い換えることができる。
3.デルタ関数は、偶関数に似た性質を持つ。
δ(x)=δ(−x)
デルタ関数の用途
電荷密度と電荷
なぜ電荷密度をデルタ関数で表せるのか
位置zに電荷eの電子が存在する。この場合、電荷密度ρ(r)と電荷eの関係は、デルタ関数を使って次のように書ける。
ρ(r)=eδ3(r−z)
位置z以外には電荷は全くないため、電荷密度は0である。そして、位置zという無限小の空間に電荷eが存在するため、位置zでのみ電荷密度が無限大に発散してしまう。だから、電荷密度をデルタ関数で表せる。
電荷密度を全空間で積分してみる
電荷密度を全空間で積分すると、全空間における電荷の総量が求まるはずだ。今考えている状況では、電荷eが1つしか存在しないため、積分結果もeになるはずだ。実際に計算してみる。
∫ρ(r)d3r=∫eδ3(r−z)d3r=e∫δ3(r−z)d3r=e･1=e
これで、計算結果がeになることが確かめられた。
参考文献
・砂川重信(1987)『物理テキストシリーズ4 電磁気学』,岩波書店.
関連記事(広告含む)
