ラプラス変換とは、下のような変換\(F(s)\)を指す。
$$F(s)=\int_0^∞ f(t)e^{-st}dt$$
ラプラス変換前の関数\(f(t)\)は\(t\)に依存している関数であるが、ラプラス変換後の関数\(F(s)\)は\(s\)に依存している関数になっている。
目次
なぜラプラス変換を考えるのか
ラプラス変換の利点は、微分方程式を代数方程式に変換して計算できることである。下の例題2では、電気回路という物理的な例を持ち出して、実際に微分方程式を代数方程式に変換して解いてみる。
例題1 ラプラス変換の方法
実際に次の関数をラプラス変換をしてみる。ただの簡単な積分の問題である。
$$f(t)=e^{αt}$$
ただし、\(s-α\)が正という前提のもと計算した。そうでないと\(\displaystyle \lim_{ t \to \infty }e^{(α-s)t}\)が\(0\)に収束しない。
ラプラス変換表について
ラプラス変換をいちいち計算するのは面倒ということで、ラプラス変換をする前とした後の関数をまとめた表が存在する。この表をラプラス変換表という。下の例題を解くときにも十分役に立つだろう。
ただし、この表はすでにネット上に大量に存在するため、ここには書かない。もし必要ならば、適当に検索するだけですぐに出てくる。参考までに、参考文献に管理人がよく利用するラプラス変換表のサイトのリンクを載せておく。
例題2 LR回路
微分方程式の例として、LR回路に流れる電流を考える。これは前の記事で微分方程式を使って解いたため、そちらも併せて参考にすることをおすすめする。
(リンク:「コイル・抵抗・コンデンサーの特徴」) 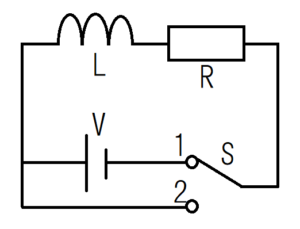
この問題では、時刻\(t=0\)でスイッチ1を入れたときの電流\(i(t)\)を考える。スイッチ2は使わない。
最初に断っておくが、このページでは、ラプラス変換する前の電流を小文字の\(i(t)\)で、ラプラス変換した後の電流を大文字の\(I(s)\)で表すことにする。電流は、ラプラス変換前は時刻\(t\)に、変換後は\(s\)に依存していることに注意すれば、両者を混同しにくくなるだろう。
ラプラス変換と代数方程式
LR回路の電流\(i(t)\)を微分方程式を使って書くと、次のように書ける。
$$L\frac{di(t)}{dt}+Ri(t)=V$$
これをラプラス変換表を使ってラプラス変換すると、次のようになる。
$$L(sI(s)-i(0))+RI(s)=\frac{V}{s}$$
ここで、定数\(V\)も、\(\frac{V}{s}\)と変換されることに注意する。また、今回は初期条件として、時刻\(t=0\)で電流が流れていない状態を考えるから、\(i(0)=0\)を代入する。
$$LsI(s)+RI(s)=\frac{V}{s}$$
この代数方程式を、\(I(s)\)で解く。
部分分数分解
ここで、ラプラス変換表にあてはめやすくするために、\(\frac{1}{s(1+\frac{L}{R}s)}\)を部分分数分解する。\(A\)と\(B\)を定数として、\(\frac{1}{s(1+\frac{L}{R}s)}\)を次のように分解することを考える。
\(A\)と\(B\)を含む項の分母をはらうために、両辺に\(s(1+\frac{L}{R}s)\)をかける。
$$1=A\left( 1+\frac{L}{R}s \right)+Bs$$
上の式はどんな\(s\)を代入しても成り立つはずである。だから、右辺の2つの項のどちらかが消えるような\(s\)を代入すれば、定数\(A\),\(B\)が求まる。
\(s=0\)を代入すると、\(Bs=0\)だから、下のように定数\(A\)が求まる。
$$1=A \left( 1+\frac{L}{R}・0 \right)+B・0$$
$$A=1$$
\(s=-\frac{R}{L}\)を代入すると、\(A \left( 1+\frac{L}{R}s \right)=0\)だから、下のように定数\(B\)が求まる。
$$B=-\frac{L}{R}$$
ここで求めた定数\(A\),\(B\)を代入すると、求めたい部分分数分解が完了する。
ラプラス変換後の電流
したがって、ラプラス変換後の電流は、次のように求まる。
ラプラス変換前の電流
後はこれを、ラプラス変換表に基づいて、ラプラス変換前の電流\(i(t)\)に直せばよい。
$$i(t)=\frac{V}{R}(1-e^{-\frac{R}{L}t})$$
この結果は、微分方程式で解いたときの電流と一致する。
何度も注意するが、ラプラス変換後の電流\(I(s)\)は\(s\)に、ラプラス変換前の電流\(i(t)\)は時刻\(t\)に依存していることを意識する。
まとめ
・ラプラス変換は、微分方程式を代数方程式に変える。
・ラプラス変換表を使えば、ラプラス変換を使った計算がスムーズに行える。
参考文献
・金沢工業大学(2009)「ラプラス変換表」,(http://w3e.kanazawa-it.ac.jp/math/category/bibun/Laplace-henkan/henkan-tex.cgi?target=/math/category/bibun/Laplace-henkan/laplace_henkan_taiouhyou.html),最終アクセス日2017/11/23.
・矢野健太郎・石原繁(編)(2009)『微分積分』,裳華房.

