[mathjax]
この記事では、s偏向とp偏向、ブリュスター角の概要と、それぞれの偏光の電磁波が誘電体に入射したときの反射率・透過率を考える。
参考:ポインティングベクトルの意味と絶対値
参考:反射の法則とスネルの法則の導出
偏光とは
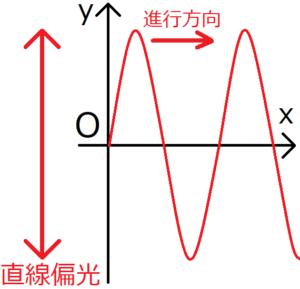
偏光方向とは、波の振幅の向きのことである。上の図でいうと、偏光方向はy軸方向となる。
波の進行方向と偏光方向は完全に別物なので注意すること。
p偏光とs偏光の違い
p偏光とs偏光の違いを、順を追って説明する。
入射面とは
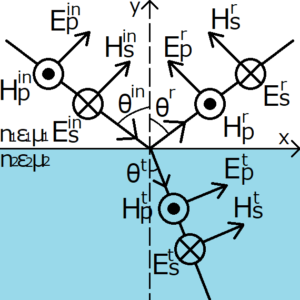
上の図は、屈折率\(n_1\)の媒質中を通る電磁波が、屈折率\(n_2\)の媒質に入射する様子を表している。
入射面とは、媒質の境界面に垂直で、かつ入射光と反射光を含むような面のことを指す。つまり、上の図でいうとxy平面のことである。
p偏光とs偏光の違い
電磁波には、p偏光とs偏光の2種類が存在する。
p偏光とは、入射面上で振動するような偏光のことを指す。一方のs偏光は、入射面に対して垂直方向に振動するような偏光のことを指す。
電磁波の振動面は、一般的に電場の振動面とされている。したがって、電場の偏光方向が入射面上にある場合、その偏光を電磁波のp偏光とする。逆に、電場の偏光方向が入射面に対して垂直である場合、その偏光を電磁波のs方向とする。改めて上の図を見ると、電場と磁場の添え字はこれに従っていることを確認できる。(ちなみに、磁場の振動面は偏光面とよばれる)
また、どちらの偏光でも、電磁波の進行方向(ポインティングベクトル\(\bf S\)の向き)と、電場と磁場の偏光方向が、下のポインティングベクトルの外積の関係を満たしていることに注意する。
$${\bf S}(t,{\bf r})={\bf E}(t,{\bf r})×{\bf H}(t,{\bf r})$$
なぜ2つの偏光を意識するのか
2つの偏光に分けて考える理由は、それぞれの偏光で反射率・透過率が異なるからである。次に、その違いについて考える。
p偏光の反射率と透過率の導出
まず、p偏光(電場が入射面上にある場合)について考える。
x,y成分の電場の境界条件
電場と磁場の境界条件より、境界面\(y=0\)において、次の関係が成り立つ。
$$E_p^{in}+E_p^r=E_p^t$$
$$B_p^{in}+B_p^r=B_p^t$$
参考:電場と磁場の境界条件
また、p偏光では電場はxy平面上で振動するから、\(E_p^{in},E_p^r,E_p^t\)をそれぞれx,y成分に分解できる。境界面に対して平行な電場は連続であるという境界条件より、x成分の境界条件は次のように書き換えられる。
$$E_p^{in}cosθ^{in}-E_p^rcosθ^r=E_p^tcosθ^t・・・(1)$$
\(E_p^r\)だけx軸方向とは逆向きになっているので、マイナスを付ける必要がある。
さらに、境界面に対して垂直方向の電束密度は連続であるという境界条件より、y成分の境界条件が次のように求まる。
$$-ε_1(E_p^{in}sinθ^{in}+E_p^rsinθ^r)=-ε_2E_p^tsinθ^t・・・(2)$$
また、反射の法則より次の関係が成り立つ。
$$θ^{in}=θ^r$$
参考:反射の法則とスネルの法則の導出
以降、
$$θ≡θ^{in}=θ^r,$$
とおく。これに従って式(1)と式(2)を書き換える。
$$E_p^{in}cosθ-E_p^rcosθ=E_p^tcosθ^t・・・(3)$$
$$ε_1(E_p^{in}+E_p^r)sinθ=ε_2E_p^tsinθ^t・・・(4)$$
反射係数と透過係数
p偏光の電場の反射係数\(r_p\)と透過係数\(r_t\)はそれぞれ、入射光と反射光・透過光の振幅の比で定義される。次のように定義される。後述するが、反射係数と反射率、透過係数と透過率は違うものである。
$$r_p≡\frac{E_p^r}{E_p^{in}}$$
$$t_p≡\frac{E_p^t}{E_p^{in}}$$
\(r_p,t_p\)を求めるには、まず式(3)と式(4)を連立方程式とみなして、\(\frac{E_p^r}{E_p^{in}},\frac{E_p^t}{E_p^{in}}\)について解く。この連立方程式は、両辺を\(E_p^{in}\)で割ったあと、以下のように行列式で考えるのが楽だろう。
$$\left( \begin{array}{c} cosθ \\ ε_1sinθ \end{array} \right)=\begin{pmatrix} cosθ & cosθ^t \\ -ε_1sinθ & ε_2sinθ^t \end{pmatrix} \left( \begin{array}{c}\frac{E_p^r}{E_p^{in}} \\ \frac{E_p^t}{E_p^{in}} \end{array} \right)$$
上の2×2行列の逆行列を、両辺の左側からかける。
\begin{eqnarray} \left( \begin{array}{c}\frac{E_p^r}{E_p^{in}} \\ \frac{E_p^t}{E_p^{in}} \end{array} \right)&=&\begin{pmatrix} cosθ & cosθ^t \\ -ε_1sinθ & ε_2sinθ^t \end{pmatrix}^{-1} \left( \begin{array}{c} cosθ \\ ε_1sinθ \end{array} \right)\\&=&\frac{1}{ε_2cosθsinθ^t-(-ε_1cosθ^t sinθ)}\begin{pmatrix} ε_2sinθ^t & -cosθ^t \\ ε_1sinθ & cosθ \end{pmatrix} \left( \begin{array}{c} cosθ \\ ε_1sinθ \end{array} \right)\\&=&\frac{1}{ε_2cosθsinθ^t+ε_1cosθ^t sinθ} \left( \begin{array}{c} ε_2sinθ^tcosθ-ε_1cosθ^tsinθ \\ ε_1sinθcosθ+ε_1cosθsinθ \end{array} \right)\\&=&\frac{1}{ε_2cosθsinθ^t+ε_1cosθ^t sinθ} \left( \begin{array}{c} ε_2sinθ^tcosθ-ε_1cosθ^tsinθ \\ 2ε_1sinθcosθ \end{array} \right) \end{eqnarray}
したがって、
$$r_p=\frac{ε_2sinθ^tcosθ-ε_1cosθ^tsinθ}{ε_2cosθsinθ^t+ε_1cosθ^t sinθ}$$
$$t_p=\frac{2ε_1sinθcosθ}{ε_2cosθsinθ^t+ε_1cosθ^t sinθ}$$
となる。
反射係数と透過係数の変形
\(r_p\)と\(t_p\)をもう少しわかりやすい形にしてみよう。
これらに含まれる誘電率\(ε_1,ε_2\)を、スネルの法則
$$n_1sinθ=n_2sinθ^t$$
を使って変形させる。このスネルの法則の式は、\(μ_0=μ_1=μ_2\)を仮定すると、
$$n=\frac{c}{v}=\sqrt{\frac{εμ}{ε_0μ_0}}$$
より、
$$\sqrt{ε_1}sinθ=\sqrt{ε_2}sinθ^t$$
と変形できる。
\begin{eqnarray} r_p&=&\frac{ε_2sinθ^tcosθ-ε_1cosθ^tsinθ}{ε_2cosθsinθ^t+ε_1cosθ^t sinθ}\\&=&\frac{\frac{ε_2}{ε_1}sinθ^tcosθ-cosθ^tsinθ}{\frac{ε_2}{ε_1}cosθsinθ^t+cosθ^t sinθ}\\&=&\frac{\frac{sin^2θ}{sin^2θ^t}sinθ^tcosθ-cosθ^tsinθ}{\frac{sin^2θ}{sin^2θ^t}cosθsinθ^t+cosθ^t sinθ}\\&=&\frac{\frac{sinθ}{sinθ^t}cosθ-cosθ^t}{\frac{sinθ}{sinθ^t}cosθ+cosθ^t}\\&=&\frac{sinθcosθ-sinθ^tcosθ^t}{sinθcosθ+sinθ^tcosθ^t}\\&=&(sinθcosθ-sinθ^tcosθ^t)・\frac{1}{sinθcosθ+sinθ^tcosθ^t}\\&=&\frac{sinθcosθ-sinθ^tcosθ^t}{sin^2θ-sin^2θ^t}・\frac{sin^2θ-sin^2θ^t}{sinθcosθ+sinθ^tcosθ^t}\\&=&\frac{\frac{2sinθcosθ}{2}-\frac{2sinθ^tcosθ^t}{2}}{\frac{1}{2}(1-cos2θ)-\frac{1}{2}(1-cos2θ^t)}・\frac{\frac{1}{2}(1-cos2θ)-\frac{1}{2}(1-cos2θ^t)}{\frac{2sinθcosθ}{2}+\frac{2sinθ^tcosθ^t}{2}}\\&=&\frac{2sinθcosθ-2sinθ^tcosθ^t}{(1-cos2θ)-(1-cos2θ^t)}・\frac{(1-cos2θ)-(1-cos2θ^t)}{2sinθcosθ+2sinθ^tcosθ^t}\\&=&\frac{sin2θ-sin2θ^t}{-(cos2θ-cos2θ^t)}・\frac{-(cos2θ-cos2θ^t)}{sin2θ+sin2θ^t}\\&=&\frac{2sin\left(\frac{2θ-2θ^t}{2}\right)cos\left(\frac{2θ+2θ^t}{2}\right)}{-\left(-2sin\left(\frac{2θ+2θ^t}{2}\right)sin\left(\frac{2θ-2θ^t}{2}\right)\right)}・\frac{-\left(-2sin\left(\frac{2θ+2θ^t}{2}\right)sin\left(\frac{2θ-2θ^t}{2}\right)\right)}{2sin\left(\frac{2θ+2θ^t}{2}\right)cos\left(\frac{2θ-2θ^t}{2}\right)}\\&=&\frac{cos\left(θ+θ^t\right)}{sin\left(θ+θ^t\right)}・\frac{sin\left(θ-θ^t\right)}{cos\left(θ-θ^t\right)}\\&=&\frac{1}{tan(θ+θ^t)}・tan(θ-θ^t)\\&=&\frac{tan(θ-θ^t)}{tan(θ+θ^t)}\end{eqnarray}
\begin{eqnarray} t_p&=&\frac{2ε_1sinθcosθ}{ε_2cosθsinθ^t+ε_1cosθ^t sinθ}\\&=&\frac{2sinθcosθ}{\frac{ε_2}{ε_1}cosθsinθ^t+cosθ^t sinθ}\\&=&\frac{2sinθcosθ}{\frac{sin^2θ}{sin^2θ^t}cosθsinθ^t+cosθ^t sinθ}\\&=&\frac{2sinθ^tcosθ}{sinθcosθ+sinθ^tcosθ^t}\\&=&\frac{2sinθ^tcosθ}{\frac{2sinθcosθ}{2}+\frac{2sinθ^tcosθ^t}{2}}\\&=&\frac{4sinθ^tcosθ}{2sinθcosθ+2sinθ^tcosθ^t}\\&=&\frac{4sinθ^tcosθ}{sin2θ+sin2θ^t}\\&=&\frac{4sinθ^tcosθ}{2sin\left( \frac{2θ+2θ^t}{2} \right) cos \left( \frac{2θ-2θ^t}{2} \right)}\\&=&\frac{2sinθ^tcosθ}{sin(θ+θ^t) cos(θ-θ^t)} \end{eqnarray}
まとめると、
$$r_p=\frac{tan(θ-θ^t)}{tan(θ+θ^t)}$$
$$t_p=\frac{2sinθ^tcosθ}{sin(θ+θ^t) cos(θ-θ^t)} $$
反射率と透過率
反射係数と透過係数が振幅の比を表しているのに対して、反射率と透過率は、入射光のエネルギーに対する反射光・透過光のエネルギーの比を表している。
電磁波のエネルギーは、ポインティングベクトル
$${\bf S}={\bf E}×{\bf H}$$
で表された。このポインティングベクトルの時間平均した絶対値\(|\bar{\bf S}|\)は、次のようになる。
$$|\bar{\bf S}|=\sqrt{\frac{ε}{μ}}|E|^2$$
参考:ポインティングベクトルの意味と絶対値
光の屈折が起こると、それに伴って電磁波の断面積が変化するため、反射係数\(r\)と反射率\(R\)、透過係数\(t\)と透過率\(T\)の関係はそれぞれ次のようになる。
\begin{eqnarray}R&=&\frac{\sqrt{\frac{ε_1}{μ_1}}E^rcosθ}{\sqrt{\frac{ε_1}{μ_1}}E^{in}cosθ}\\&=&r^2\end{eqnarray}
\begin{eqnarray}T&=&\frac{\sqrt{\frac{ε_2}{μ_2}}E^tcosθ^t}{\sqrt{\frac{ε_1}{μ_1}}E^{in}cosθ}\\&=&\frac{n_2cosθ^t}{n_1cosθ}t^2\end{eqnarray}
つまり、p偏光の反射率\(R_p\)と透過率\(T_p\)は、それぞれ次のようになる。
\begin{eqnarray}R_p&=&r_p^2\\&=&\frac{tan^2(θ-θ^t)}{tan^2(θ+θ^t)}\end{eqnarray}
\begin{eqnarray}T_p&=&\frac{n_2cosθ^t}{n_1cosθ}t_p^2\\&=&\frac{sinθcosθ^t}{sinθ^tcosθ}\frac{4sin^2θ^tcos^2θ}{sin^2(θ+θ^t) cos^2(θ-θ^t)}\\&=&\frac{4sinθcosθsinθ^tcosθ^t}{sin^2(θ+θ^t) cos^2(θ-θ^t)}\\&=&\frac{sin2θsin2θ^t}{sin^2(θ+θ^t) cos^2(θ-θ^t)} \end{eqnarray}
ブリュースター角とは

ブリュースター角とは、入射角が0度から90度までの範囲において、反射率が0になるような入射角のことである。
反射率の式
$$R_p=\frac{tan^2(θ-θ^t)}{tan^2(θ+θ^t)}$$
の分母に注目すると、\(θ+θ^t=\frac{π}{2}\)を満たすときに分母が無限大に発散することがわかる。つまり、この条件を満たす場合、反射率\(R\)は0となる。
このときの\(θ\)をブリュースター角という。この入射角において、p偏光の電場はすべて透過することになるため、透過率は\(T=1\)になる。
ちなみに、入射する媒質のほうが屈折率が低く、全反射する場合は、上のグラフは次のようになる。

s偏光の反射率と透過率の導出
次に、s偏光(電場が入射面に対して垂直に偏光する場合)について考える。
電場と磁場(今回は磁束密度ではない)の境界条件より、p偏光と同様に\(μ_0=μ_1=μ_2\)を仮定すると、次の関係がいえる。
$$E_s^{in}+E_s^r=E_s^t$$
$$-\sqrt{ε_1}E_s^{in}cosθ+\sqrt{ε_1}E_s^rcosθ=-\sqrt{ε_2}E_s^tcosθ^t$$
この2式の両辺を\(E_0^{in}\)で割り、行列式にまとめる。
$$\left( \begin{array}{c} 1 \\ \sqrt{ε_1}cosθ \end{array} \right)=\begin{pmatrix} -1 & 1 \\ \sqrt{ε_1}cosθ & \sqrt{ε_2}cosθ^t \end{pmatrix} \left( \begin{array}{c}\frac{E_p^r}{E_p^{in}} \\ \frac{E_p^t}{E_p^{in}} \end{array} \right)$$
上の2×2行列の逆行列を、両辺の左側からかけて、反射係数\(r_s\)と透過係数\(t_s\)が求まる。
\begin{eqnarray}\left( \begin{array}{c}\frac{E_p^r}{E_p^{in}} \\ \frac{E_p^t}{E_p^{in}} \end{array} \right)&=&\begin{pmatrix} -1 & 1 \\ \sqrt{ε_1}cosθ & \sqrt{ε_2}cosθ^t \end{pmatrix}^{-1}\left( \begin{array}{c} 1 \\ \sqrt{ε_1}cosθ \end{array} \right)\\&=& \frac{1}{-\sqrt{ε_2}cosθ^t-\sqrt{ε_1}cosθ} \begin{pmatrix} \sqrt{ε_2}cosθ^t & -1 \\ -\sqrt{ε_1}cosθ & -1 \end{pmatrix}\left( \begin{array}{c} 1 \\ \sqrt{ε_1}cosθ \end{array} \right)\\&=& \frac{1}{-\sqrt{ε_2}cosθ^t-\sqrt{ε_1}cosθ} \begin{pmatrix} \sqrt{ε_2}cosθ^t & -1 \\ -\sqrt{ε_1}cosθ & -1 \end{pmatrix}\left( \begin{array}{c} 1 \\ \sqrt{ε_1}cosθ \end{array} \right)\\&=&\frac{1}{\sqrt{ε_1}cosθ+\sqrt{ε_2}cosθ^t} \left( \begin{array}{c} \sqrt{ε_1}cosθ-\sqrt{ε_2}cosθ^t \\ 2\sqrt{ε_1}cosθ \end{array} \right) \end{eqnarray}
したがって、スネルの法則を使うと反射率\(R_s\)が次のように求まる。
\begin{eqnarray}R_s&=&r_s^2\\&=&\left( \frac{\sqrt{ε_1}cosθ-\sqrt{ε_2}cosθ^t}{\sqrt{ε_1}cosθ+\sqrt{ε_2}cosθ^t} \right)^2\\&=&\left( \frac{\frac{\sqrt{ε_1}}{\sqrt{ε_2}}cosθ-cosθ^t}{\frac{\sqrt{ε_1}}{\sqrt{ε_2}}cosθ+cosθ^t} \right)^2\\&=&\left( \frac{\frac{sinθ^t}{sinθ}cosθ-cosθ^t}{\frac{sinθ^t}{sinθ}cosθ+cosθ^t} \right)^2\\&=&\left( \frac{sinθ^tcosθ-sinθcosθ^t}{sinθ^tcosθ+sinθcosθ^t} \right)^2\\&=&\left( -\frac{sin(θ-θ^t)}{sin(θ+θ^t)} \right)^2\\&=&\frac{sin^2(θ-θ^t)}{sin^2(θ+θ^t)}\end{eqnarray}
また、透過率\(T_s\)は、
\begin{eqnarray} T_s&=&\frac{n_2cosθ^t}{n_1cosθ}t^2\\&=&\frac{n_2cosθ^t}{n_1cosθ} \left(\frac{2\sqrt{ε_1}cosθ}{\sqrt{ε_1}cosθ+\sqrt{ε_2}cosθ^t}\right)^2\\&=&\frac{n_2cosθ^t}{n_1cosθ} \left(\frac{2cosθ}{cosθ+\sqrt{\frac{ε_2}{ε_1}}cosθ^t}\right)^2\\&=&\frac{n_2cosθ^t}{n_1cosθ} \left(\frac{2cosθ}{cosθ+\frac{sinθ}{sinθ^t}cosθ^t}\right)^2\\&=&\frac{n_2cosθ^t}{n_1cosθ} \left(\frac{2sinθ^tcosθ}{sinθ^tcosθ+sinθcosθ^t}\right)^2\\&=&\frac{n_2cosθ^t}{n_1cosθ} \left(\frac{2sinθ^tcosθ}{sin(θ+θ^t)}\right)^2\\&=&\frac{sinθcosθ^t}{sinθ^tcosθ}\frac{4sin^2θ^tcos^2θ}{sin^2(θ+θ^t)}\\&=&\frac{sin2θ^tcos2θ}{sin^2(θ+θ^t)} \end{eqnarray}
まとめ
・反射係数と透過係数は振幅の比、反射率と透過率はエネルギーの比を表す。
参考文献
・伊東敏雄(2008)『朝倉物理学選書2 電磁気学』,朝倉書店.
・砂川重信(1988)『電磁気学 ―初めて学ぶ人のために―』,培風館.





