[mathjax]
前の記事では電荷とは何かを考えたが、この電荷は、周囲の空間に影響を及ぼすことができる。このような周囲の空間への影響のことを一般的に場とよぶのだが、特に電荷がつくる場のことを電場という。
この記事では、一つの電荷が作り出す電場について考える。
参考:電荷とクーロンの法則
電場の定義
2つの電荷の間にはクーロン力が働く。
ここで、電荷\(q_2\)が発生させる電場\(E\)を、式(1)を使って定義したい。電荷\(q_1\)が\(q_2\)から受けるクーロン力の式(1)に注目すると、クーロン力\(F\)と電荷\(q_1\)の間の関係について、\(\frac{1}{4πε_0}\frac{q_2}{r^2}\)を一つの関数\(E(r)\)と定義すれば、式(1)を下のような簡単な形で書き直せる。この関数\(E(r)\)のことを電場とよぶ。
式(1)の左辺の力\(F\)はスカラー量となっているが、一般的に力は3次元のベクトル量\(\bf F\)で表される。\(q_1\)は明らかにスカラー量だから、もし力をベクトル量\(\bf F\)にした場合、電場がベクトル量\({\bf E}({\bf r})\)となる。
式(2)より、クーロン力と電場は平行である。
電場の向きと電荷
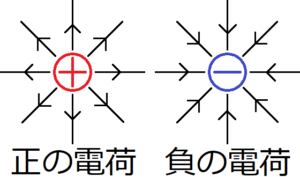
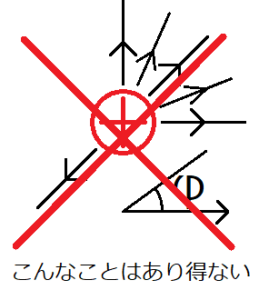
クーロン力の式(1)より、2つの電荷の値\(q_1,q_2\)が変化しない場合のクーロン力\(F\)の大きさは、電荷間の距離\(r\)にのみ依存する。つまり、電荷の位置を原点とした極座標を考えると、クーロン力は角度に依存しない。このことと、クーロン力と電場が平行であることを考慮すると、電場\(\bf E\)は、電荷\(q_2\)に対して放射状かつ均等に広がっていくことが予想される。
電場の向きについて
電場の向きは、電荷の種類によって上の図のように定義される。
言葉で言い換えると、正の電荷による電場は、その電荷から放射状に広がる方向に定義される。一方負の電荷による電場は、その電荷に向かっていく方向に定義される。
2つの電荷を結ぶ電気力線
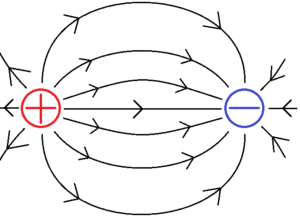
電気力線とは、電場の向きを線でつなぐことで、電場の流れを直感的にわかりやすく表したものである。この電気力線は、等電位線とは常に垂直に交わる。
まとめ
・クーロン力の式から電場を定義した。
・電気力線とは何かを確認した。
参考文献
・伊東敏雄(2008)『朝倉物理学選書2 電磁気学』,朝倉書店.
・砂川重信(1987)『物理テキストシリーズ4 電磁気学』,岩波書店.
・砂川重信(1988)『電磁気学 ―初めて学ぶ人のために―』,培風館.

