アンペールの法則とは、閉曲面を垂直に通過する電流と、その周りに発生する磁束密度に関する法則のことである。この法則は、マクスウェル方程式の一つとされるほど重要なものである。
この記事では、アンペールの法則について考える。
目次
前提知識 立体角
立体角\(dΩ\)とは、任意の点\(P\)からみた半径\(r\)の球面の面積のことである。
ガウスの法則の導出にも立体角を使ったので、詳しくは下の記事を参照のこと。
参考:ガウスの法則の導出
アンペールの法則の証明
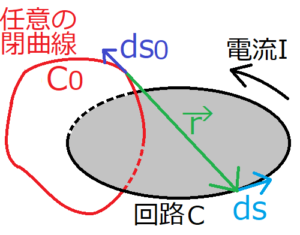
以降、上の図のように、任意の閉曲線\(C_0\)の中に回路\(C\)が通っている状況を考える。
ビオサバールの法則の積分(間違えた例)
この節の説明には欠陥が含まれているので注意すること。どこが変なのか考えながら読んでみよう。
ビオサバールの法則とは、微小距離\(d{\bf s}\)を流れる電流がつくる磁束密度を表す法則のことである。
参考:ビオ・サバールの法則
この両辺を回路\(C\)で線積分すると、閉曲線\(C_0\)上のベクトル\(ds_0\)における磁束密度が求まる。
さらに、この式の両辺を閉曲線\(C_0\)で線積分すれば、閉曲線\(C_0\)全体における磁束密度が求まる。
注意:この式(1)の導出には、後述するような重大な欠陥がある。この時点でそれに気づけたらすごい(管理人は半日考え込んだ)。
式(1)の導出の欠陥とは
この式(1)には重大な欠陥がある。それは、位置ベクトルの出発点を閉曲線\(C_0\)上のベクトル\(ds_0\)にしてしまったことで、閉曲線\(C_0\)で線積分するときに、位置ベクトル\(\bf r\)の出発点が動くことである。式(1)の導出によると、ベクトル\(\bf r\)の出発点と到着点の両方が、線積分によって動くことになってしまう。
ベクトルを使った線積分の前提条件として、位置ベクトルの出発点が固定されていることが挙げられる。したがって、ベクトル\(\bf r\)の出発点を固定する必要がある。
位置ベクトル\(r\)の出発点の固定方法
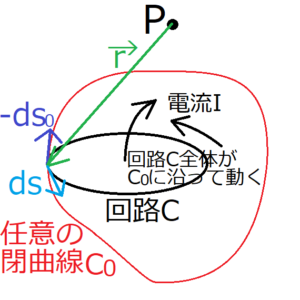
では、どのようにすればその出発点を固定できるのだろうか。まず、ベクトル\(\bf r\)出発点を、任意の場所に固定する。そして、回路\(C\)全体を、\(ds_0\)とは逆方向に動かせばよい。こうすれば、回路が\(C_0\)に沿って動いたときの、点\(P\)における磁束密度が求まる。
固定する位置ベクトル\(\bf r\)の出発点を点\(P\)とする。ここからビオサバールの法則の式を回路\(C\)で線積分するまでは、前と同じである。ただし、今回は点\(P\)における磁束密度の大きさを考えているため、\(\bf r\)にマイナスをつけなければならない。
前述したとおり、閉曲線\(C_0\)上の線積分の方向は逆向きとなるから、下の\(C_0\)についての線積分の微小部分\(ds_0\)にはマイナスがつく。
立体角\(dΩ\)の定義について
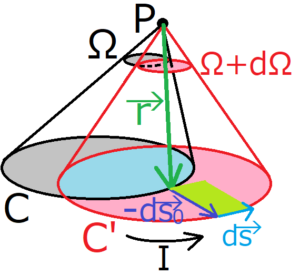
上の図のような、立体角\(Ω\)の微小変化を考える。点\(P\)から見た回路\(C\)の立体角の変化\(dΩ\)について考える。
2つのベクトルを辺とする平行四辺形の面積は、そのベクトルの外積で表される。これを利用すると、上の図の黄緑色の平行四辺形の面積ベクトルは、次のように書ける。
ただし、面積ベクトル\(d{\bf S}\)の向きが上図でいう上向きになるようにした。
この面積ベクトルを回路\(C\)で線積分すれば、立体角の定義式の\(dS\)に代入できるようになる。
外積の順序を入れ替えると正負が逆になるから、
後は、3重積のベクトルの公式\(({\bf A}×{\bf B})・{\bf C}=({\bf B}×{\bf C})・{\bf A}\)を使えば、\(dΩ\)が式(2)に代入できるような形になる。
アンペールの法則の導出
式(2)に式(3)の立体角\(dΩ\)を導入する。
球の中心から見た球面全体の立体角は\(4π\)だから、
この式をまとめると、
この式が、アンペールの法則と呼ばれる式である。
任意の閉曲線\(C_0\)上における磁束密度の線積分は、電流\(I\)が閉曲線を貫く場合、真空中の透磁率と電流の積に等しくなる。
今回は定常電流\(I\)が流れる場合について考えた。これに加えて電荷保存則も考慮することで、電場を含む一般的なアンペールの法則を導くことができる。これについては後日記事にする予定である。
まとめ
・ビオサバールの法則の式を積分することで、アンペールの法則を導いた。ここで、位置ベクトル\(\bf r\)の出発点を固定するために、回路ごと移動させる考えを使った。
参考文献
・伊東敏雄(2008)『電磁気学 (朝倉物理学選書)』,朝倉書店.
・砂川重信(1987)『電磁気学 (物理テキストシリーズ 4)』,岩波書店.
・砂川重信(1988)『電磁気学―初めて学ぶ人のために』,培風館.

