[mathjax]
$$E=mc^2$$
この式は、アインシュタインによって導かれた式として非常に有名である。Eはエネルギー、mは質量、cは光速度である。つまり、この式はエネルギーと質量の等価式だといえる。
この記事では、この式の導出と意味について考察する。
相対性理論
双子のパラドックスの解き方
前の記事では、静止している系から運動している系の時計を見ると、時刻が遅れて見えることを確認した。
参考:ローレンツ変換の意味
ところが、運動系から見ると静止系は動いて見えるため、運動系からも静止系の時計は遅れて見えるはずである。これでは、互いに相手の時計が遅れて見えることになり、矛盾が生じる。
この問題は、地球にいる双子の弟と光速に近い速度のロケットに乗っている兄が再開したとき、どちらが年上か、という問題に置き換えられる。これを、双子のパラドックスという。この記事では、ミンコフスキー空間を使って双子のパラドクスを解いてみる。
世界間隔の共変性と固有時について
世界間隔Δsとは、ミンコフスキー空間内の2点間の距離のことである。式で表すと次のようになる。
$$(Δs)^2=-c^2(t_1-t_2)^2+({\bf r}_1-{\bf r}_2)^2$$
この世界間隔は、ローレンツ変換に対して不変である。このことはつまり、世界間隔は慣性系によらず一定であることを意味する。このように、ローレンツ変換を施しても値が変わらない性質のことを、ローレンツ変換に対して共変的であるという。
また、\(ds\)を次のように定義する。
$$ds^2≡dx^2+dy^2+dz^2-c^2dt^2$$
\(dx=v_xdt\)に注意して、\(v=\sqrt{v_x^2+v_y^2+v_z^2}\)とおくと、
$$\sqrt{-ds^2}=\sqrt{c^2-v^2}dt$$
固有時\(dτ\)を次のように定義すると、次のように変形できる。
$$dτ≡\frac{\sqrt{-ds^2}}{c}=\sqrt{1-\left( \frac{v}{c} \right)^2 }dt$$
この固有時もローレンツ変換に対して不変である。
ミンコフスキー空間とは
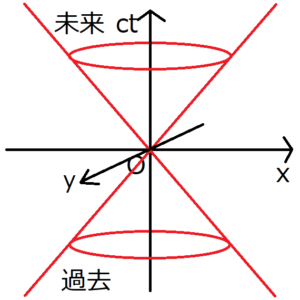
ミンコフスキー空間とは、横軸に場所、縦軸に時間をとり、原点に観測者を置いた空間のことである。ミンコフスキー空間上の直線の傾きは、物体の速度を表す。特に、縦軸を\(ct\)でとっているため、光速の傾きが45度になる。この光速を表す線を母線とする円錐を、光錐と呼ぶ。
ローレンツ収縮とその導出
静止している系から光速近くで動いている物体を観察する。すると、その物体は本来の長さ(物体が停止しているときの長さ)よりも短く見える。この現象のことをローレンツ収縮とよぶ。
物体が停止しているときの棒の長さを\(L_0\)、物体が動いている様子を静止系から見たときの棒の長さを\(L\)とすると、両者の間には次の関係が成り立つ。ただし、運動系S’は、系Sに対してx方向に速度Vの速さで動いていて、かつ棒は系S’と同じように動いているものとする。
\begin{eqnarray} L&=&L_0\sqrt{1-\frac{V^2}{c^2}}\\&=&L_0\sqrt{1-β^2} \end{eqnarray}
ローレンツ変換の意味
ほとんどの相対性理論の本は、この「ローレンツ変換」から始まる。ローレンツ変換とは、異なる動き方をしている、2つの系の時刻や空間を結びつけるような変換である。今まで学んできた力学や電磁気学などと違い、相対性理論で言っていることは、初見ではすぐには信じられないことばかりだろう。例えば、質量を持つ物体は光速に追いつけないことや、光速に近い速さで動いていると時間の進み方が遅くなることなど。この記事を読み進めることで、ローレンツ変換の意味をじっくり考えてみてほしい。