表皮効果と導体への電磁波の入射

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

[mathjax]

電磁波は、導体の表面までしか侵入できない。なぜならば、導体の内部に進むにつれて、レンツの法則によって電磁波を打ち消す方向の誘電起電力が働くからだ。この現象のことを表皮効果とよぶ。さらに、電磁波が導体に侵入できる深さの目安のことを、表皮の厚さとよぶ。

この記事では、マクスウェル方程式より表皮の厚さを求める。

1 表皮効果の模式図
2 表皮の厚さの求め方
3 まとめ
4 参考文献

表皮効果の模式図

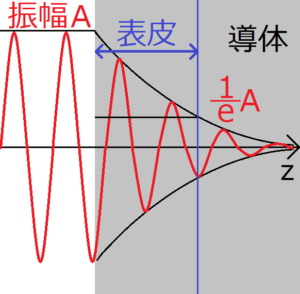
上の図の赤い線は、右方向に進む電磁波を表している。そして、導体表面から、電磁波の振幅が元の$1/e$になった地点までの距離を表皮の厚さと呼び、図の青い矢印で表されている。

表皮の厚さの求め方

オームの法則の変形

マクスウェル方程式を変形させると、以下の式が求まる。導出は下の記事を参照すること。

$$∇^2{\bf E}-με\frac{∂^2{\bf E}}{∂t^2}-μσ\frac{∂{\bf E}}{∂t}=0$$

参考:電場と磁場が満たす波動方程式

平面電磁波

また、今回は振幅$E_0$の平面電磁波を考える。

$$E=E_0e^{i(ωt-kz)}$$

参考:等位相面と平面波とは

波数$k$が満たす式

平面波$E$を、マクスウェル方程式を変形させた式に代入する。

$$-k^2E_0e^{i(ωt-kz)}+μεω^2E_0e^{i(ωt-kz)}-iμσωE_0e^{i(ωt-kz)}=0$$

両辺を$E_0e^{i(ωt-kz)}$で割る。

$$-k^2+μεω^2-iμσω=0$$

$k^2$について解く。

\begin{eqnarray}k^2&=&-iμσω+μεω^2\\&=&-iμσω\left(1+i\frac{εω}{σ}\right)･･･(1)\end{eqnarray}

ここで、外部電場$E$が準定常電流の条件

$$ω<<\frac{σ}{ε}$$

を満たす場合、式(1)の右辺第二項は無視できる。

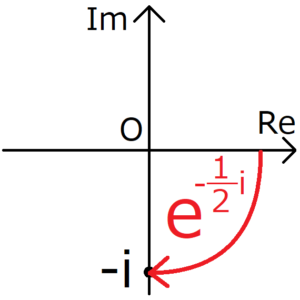
\begin{eqnarray}k^2&=&-iμσω\\&=&e^{-\frac{1}{2}i}･μσω･･･(2)\end{eqnarray}

複素平面では下の図のように、座標$-i$と座標$e^{-\frac{1}{2}i}$が対応していることに注意すること。

(ちなみに、準定常電流とは、角周波数$ω$が$\frac{σ}{ε}$に対して十分小さいため、変位電流が無視できるような交流電流のことである)

式(2)の二乗根をとり、変形させる。

\begin{eqnarray}k&=&\pm\sqrt{e^{-\frac{1}{2}i}･μσω}\\&=&\pm e^{-\frac{1}{4}i}･\sqrt{μσω}\\&=&\pm\frac{1-i}{\sqrt{2}}\sqrt{μσω}\\&=&\pm(1-i)\sqrt{\frac{μσω}{2}}･･･(3)\end{eqnarray}

複素平面上の座標$(1-i)$と座標$e^{-\frac{1}{4}i}$が対応している。$(1-i)$を$\sqrt{2}$で割っているのは、規格化して複素数の大きさを$1$に調整するためである。

表皮の厚さの導出

最後に、求めた$k$を平面波の式に代入する。式(3)より$k$は正負の2種類存在するが、そのうち$z>0$で発散しないほうの解を使う。つまり、

$$k=-(1-i)\sqrt{\frac{μσω}{2}}$$

を代入すればよい。

\begin{eqnarray}E&=&E_0e^{i(ωt-kz)}\\&=&E_0e^{i\left[ωt-\left( (1-i)\sqrt{\frac{μσω}{2}}z\right) \right]}\\&=&E_0e^{-\sqrt{\frac{μσω}{2}}z}e^{i\left(ωt+\sqrt{\frac{μσω}{2}}z \right)}\end{eqnarray}

表皮の厚さ$δ$は、導体の表面から電場の振幅が$e^{-1}$倍になる場所までの距離のことだから、指数に虚数$i$が含まれない$e^{-\sqrt{\frac{μσω}{2}}z}$に注目すれば、$δ$求まることが予想できる。

$$δ=\sqrt{\frac{2}{μσω}}$$

以上で、表皮の厚さが求めらえた。

まとめ

・表皮効果とは何か確認した。

・表皮の厚さを求めた。

参考文献

・伊東敏雄(2008)『朝倉物理学選書2 電磁気学』,朝倉書店.

・砂川重信(1988)『電磁気学 ―初めて学ぶ人のために―』,培風館.

表皮効果と導体への電磁波の入射

表皮効果の模式図