エルステッドは電流が磁気的性質をもつことを発見したが、一方ファラデーは、磁束が電流をつくることを発見した。この現象を電磁誘導とよび、またこれによって発生した電流のことを誘導電流とよぶ。
この記事では、電磁誘導について掘り下げる。
レンツの法則
コイルは、内部の磁束密度が変化することを嫌う。そのために、外的要因によって内部の磁束密度が変化した場合、その変化を打ち消すような誘導電流がコイル内に流れる。
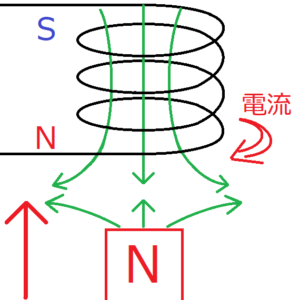
上の図のように、コイルに磁石のN極を近づける。この場合、コイルは磁石を遠ざけようとするため、磁石が近づいてくるほうをN極、反対側がS極になるような向きの電流が発生する。そしてその電流の向きは、親指をコイルのN極に向けたときの右ねじに対応する。
このように、コイル内の磁束を打ち消す方向に誘導電流が流れることをレンツの法則とよぶ。
ちなみにこの性質は、電気回路上のコイルにも当然適応される。回路上のコイルの性質については下の記事を参照すること。
ファラデーの電磁誘導の法則
実験より、次の関係が求められる。この関係をファラデーの電磁誘導の法則とよぶ。
\(N\)はコイルの巻き数、\(φ\)は誘導起電力、\(Φ\)はコイル内部を通過する磁束である(誘導電流がつくる磁束ではない)。
例題 交流発電機
一様な磁束密度中でコイルを回転させると、コイルを垂直に貫く磁束密度が絶えず変化する状況を作れるため、そのコイルに誘電起電力を発生させることができる。
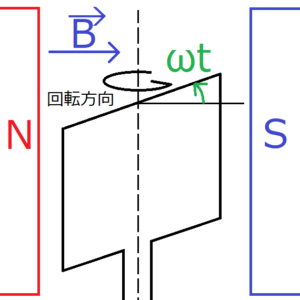
では、一様な磁束密度\(\bf B\)中で、断面積\(S\)の1巻きコイルを角速度\(ω\)で回転させたときの、コイルに発生する誘電起電力を求めてみよう。
コイルを垂直に貫く磁束とは
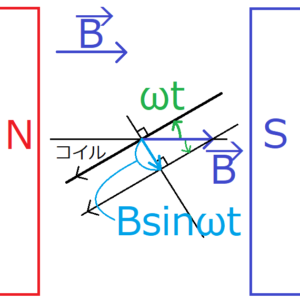
上の図は、上から見たときの交流発電機の様子を表している。ただし、補助線は細い黒線で描いた。この図から、まずはコイルの中心を垂直に貫く磁束の大きさ\(Φ_⊥\)を求めよう。
磁束密度\(\bf B\)とコイルの間の角度は\(ωt\)となる。そのため図より、コイルの中心を垂直に貫く磁束密度の大きさは\(Bsinωt\)となる。ただし、\(|{\bf B}|=B\)とおいた。
これに加えて、コイルの断面積は\(S\)で、なおかつ磁束密度\(\bf B\)は一様だから、求める磁束\(Φ_⊥\)は次のようになる。
誘導起電力の大きさ
後はファラデーの法則より、\(Φ_⊥\)を時間\(t\)で微分すれば、コイルの誘導起電力が求まる。
まとめ
・ファラデーの電磁誘導の法則の内容を確認した。
・交流発電機の起電力を計算した。
参考文献
・伊東敏雄(2008)『電磁気学 (朝倉物理学選書)』,朝倉書店.
・砂川重信(1988)『電磁気学―初めて学ぶ人のために』,培風館.

