[mathjax]
導体に電荷\(Q\)を与えると、その導体の電位が変化する。そして、このときの電位の変化量\(Δφ\)と与えた電荷量\(Q\)は比例の関係を満たす。このときの比例定数を静電容量(電気容量)といい、通常\(C\)で表す。
この記事では、静電容量について考える。
コンデンサーとは
コンデンサーとは、正に帯電した導体から出てくる電気力線が、すべて負に帯電した導体に吸い込まれる構造のことである。コンデンサーには電荷を蓄える性質がある。電気回路上のコンデンサーの性質は、下の記事を参照のこと。
平行板コンデンサー
平行板コンデンサーは、最も単純な構造をもつコンデンサーである。
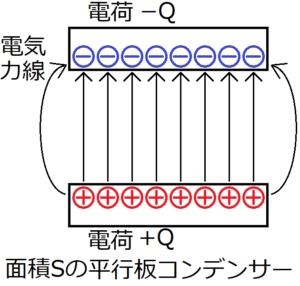
2つの面積\(S\)の導体板をそれぞれ電荷\(+Q,-Q\)に帯電させ、真空中で平行になるように向かい合わせる。すると、\(+Q\)に帯電させた導体板から出てくる電気力線は、すべてもう片方の\(-Q\)に帯電させた導体板に吸い込まれる。したがって、この導体の平行板の組はコンデンサーであるといえる。
実際の電気力線は導体板の側面から出てくるものもあるが、今回は導体板の平面から垂直に出てくる電気力線のみを考える。
一様な電場と電位の関係式
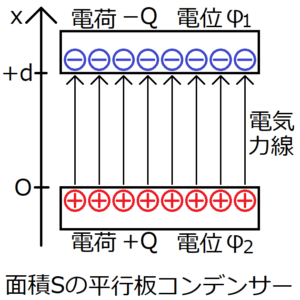
導体板に電荷を与えることで、その導体板の電位が変化する。\(-Q\)に帯電させた方の電位を\(φ_1\)、\(+Q\)に帯電させた方の電位を\(φ_2\)とおく。
また、電場と電位は次の関係を満たす。
参考:電位とは
この式をもとに、平行板による一様な電場\(E\)と電位差\(Δφ≡φ_2-φ_1\)の関係式を求める。まず、式(1)の両辺に\(dx\)をかけて、積分する。ここで、帯電させる電荷の種類から、\(φ_1<φ_2\)がいえる。
これらと式(1)より、
これで、この平行板コンデンサーにおける一様な電場と電位差の関係式が求められた。
一様な電場とガウスの法則
ガウスの法則とは、任意の閉曲面を出入りする電場と、その閉曲面中の電荷に関する法則のことである。
参考:ガウスの法則の導出
この法則を\(+Q\)に帯電させた導体板の表面に適応させることで、式(2)中の一様な電場\(E\)を、電荷\(+Q\)を使った形に変形させたい。
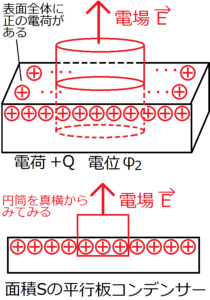
上の図のような、正の電荷を含む円柱におけるガウスの法則を考える。この円柱の底面の面積を単位面積とする。導体板の面積を\(S\)とすると、単位面積当たりの電荷は\(Q/S\)であらわされる。これを上のガウスの法則の式に代入すると、単位面積の底面をもつ円柱から出てくる電場の総和が求まる。導体の内部では電場が0となり、かつ電荷は導体の表面にのみ存在できるから、円柱の片側の底面からのみ電場が出てくることがわかる。以上のことから、この円柱をガウスの法則の面積分の積分範囲とした場合、円柱から出ていく電場は、単位面積当たりの導体板から発生する電場に等しくなることがわかる。
式(3)を式(2)に代入することで、平行板コンデンサーにおける電位と電荷の関係式が求まる。
平行板コンデンサーの電気容量
後は、一番最初の電気容量\(C\)の定義式と式(4)を比較するだけで、平行板コンデンサーの電気容量が求まる。式(4)を次のように変形すればわかりやすい。
したがって、電気容量\(C\)は、
まとめ
・電気容量の定義とコンデンサーの概要を確認した。
・最も単純なコンデンサーである平行板コンデンサーについて考えた。
参考文献
・伊東敏雄(2008)『朝倉物理学選書2 電磁気学』,朝倉書店.
・砂川重信(1987)『物理テキストシリーズ4 電磁気学』,岩波書店.
・砂川重信(1988)『電磁気学 ―初めて学ぶ人のために―』,培風館.

