量子数には、主量子数・方位量子数・磁気量子数・スピン量子数の４種類存在する。これらの量子数は、電子の軌道やスピンの大きさの指定に役立っている。この記事では、それぞれの量子数の概要についてまとめる。
前提として、電子「軌道」とはいうものの、電子は原子核の周りを円運動しているわけではないことに注意する。量子力学において、電子とは、存在確率として原子核の周りに雲のように遍在しているものとして考える。
量子力学
水素原子中の電子の波動関数と球面調和関数の導出
水素原子を球対称な物体だとすると、その原子まわりの電子の波動関数については極座標で考えたほうが理解しやすいだろう。だが、それにはシュレディンガー方程式や波動関数を極座標に変換する必要がある。
この記事では、水素原子に含まれる電子の波動関数を、シュレディンガー方程式の極座標で表してみる。まず最初に、波動関数を角度方向成分と動径方向成分に変数分離する。その後、シュレディンガー方程式を利用して、それぞれの場合における波動関数を導出する。特に角度方向の波動関数は球面調和関数と呼ばれており、物理界隈では有名なものとなっている。
なお、極座標のシュレディンガー方程式に関するハミルトニアンについては、別記事でまとめてあります。
パウリのスピン行列の導出
電子は電荷量のほかにも、角速度の次元を持ったパラメータを持っている。このパラメータのことをスピンとよぶ。このスピンを表現するために、行列式を使った固有方程式が使われる。その固有方程式中の行列のことを、スピン行列とよぶ。
この記事では、電子などの素粒子のスピン行列を導出する。
角運動量の昇降演算子の交換関係と物理的意味について
昇降演算子とは、固有方程式の固有値を変化させることができるような演算子のことである。固有値を上げるような演算子を上昇演算子、下げるような演算子を下降演算子とよぶ。
この記事では、角運動量演算子の昇降演算子の定義と、その物理的意味を紹介する。
軌道角運動量とスピン角運動量の違い
原子核のまわりに存在する電子は、軌道角運動量・スピン角運動量という２種類の角運動量をもつ。この2つの角運動量の和が、電子の総角運動量ということになる。
この記事では、これら2つの角運動量の概要を解説する。
不確定性原理の概要と導出
量子力学の有名な原理として、不確定性原理がある。これは、粒子の正確な位置と運動量を同時に観測することはできないことを意味している。
この記事では、不確定性原理の意味の解説と、期待値を利用したものと不等式を利用したものの２通りの導出について、詳しく解説する。
波束と分散について
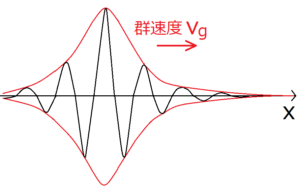
波束とは、限られた範囲にだけ存在する波のことをいう。高校までは主に全く同じ波形が無限に続くような波を考えてきたが、このような波は現実的でない。前の記事では波の重ね合わせによって生じるうなりによる群速度と位相速度について考えたが、それで学んだことは波束にも応用できる。
この記事では、古典力学の波動方程式に従う波束と、量子力学のシュレディンガー方程式に従う波束について考える。
参考:群速度と位相速度の導出
なぜE=hνが成立するのか
$$E=hν$$
この式は、光の振動数\(ν\)とエネルギー\(E\)の関係式である。\(h\)はプランク定数で、次の定数となっている。
$$h≒6.63×10^{-34} [m^2kg/s]$$
この式は量子力学で最初に出てくる重要な公式であり、量子力学の勉強はここから始まると言っても過言ではない。電子のエネルギー準位が落ちたときには、その落ち幅に対応した振動数の光が放出されることになる。この式はその光の振動数の計算に非常に役に立つ。
この記事では、なぜ上の式が成立するのかを考える。
光電効果とは
[mathjax]
光電効果には、外部光電効果と内部光電効果と光起電力効果の3種類ある。アインシュタインがノーベル賞を受賞したきっかけとなった現象としても有名でもある。
この記事では、それぞれの光電効果の概要を述べる。
ボーア半径と水素原子のエネルギー準位の導出
ラザフォードによって原子には正に帯電した原子核が存在していたことが明らかになり、その後原子のモデルとして、原子核の周りを電子が円運動している状態が提唱された。ところが、電子は円運動すると外部に電磁波を放出するため、このモデルでは次第に電子が円運動しながら原子核に近づいていくことになる。これは原子がつぶれることを意味するが、現実的にそれはありえない。
そこで、ボーアは電子を粒子ではなく波として考えて原子モデルを考えた。つまり、原子の周りで定常波をつくるような波を電子としたのだ。このようなモデルで考えた、電子を1個のみ含む水素原子の半径のことをボーア半径という。
さらに、原子核のまわりにある電子のエネルギーが離散的であることも、ボーア半径の導出に使った式を再利用することで簡単に確認できる。
この記事では、ボーア半径と、水素原子のエネルギー準位を具体的に求める。