不確定性原理の概要と導出

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

量子力学の有名な原理として、不確定性原理がある。これは、粒子の正確な位置と運動量を同時に観測することはできないことを意味している。

この記事では、不確定性原理の意味の解説と、期待値を利用したものと不等式を利用したものの２通りの導出について、詳しく解説する。

1 不確定性原理とは
2 不確定性原理による最小のばらつき
3 不等式を用いた不確定性原理の導出
- 3.1 不等式を用いた不確定性原理の証明
4 まとめ
5 参考文献

不確定性原理とは

物質波と波束の分散について

電子のような微小な粒子は、粒子としての性質と波としての性質を併せ持っている。そのため、運動している電子は、空間中を伝播している波として表現することもできる。このように、粒子を波として表したものを物質波とよぶ。その物質波の振動数$ν$は、電子のエネルギー$E$を使って次のように表せる。

$$E=hν$$

参考:なぜE=hνが成立するのか

そしてこの波の形状は、波束と呼ばれる形をしている。波束とは、限られた範囲にだけ存在する波のことをいう。波束の中で一番有名なものが、ガウス関数の形をしたものである。シュレディンガー方程式に従う波は分散を持つため、時間経過につれて波束は広くつぶれていく。ところで、物質波の絶対値の２乗は、粒子の存在確率を表した。したがって、粒子が存在しうる範囲は、時間とともに広がっていくといえる。

参考:波束と分散について

参考:シュレディンガー方程式を解く意味とは

物質波の最小の分散とは

物質波を表す波束が分散を持ち、時間とともに広がっていくことは説明した。では、初期状態の波束の分散はどうなっているのだろうか。

まず、波束の初期状態がデルタ関数のように一点に集中していることは無い。なぜならば、初期状態からある程度の広がりがなければ、物質波の振動数が求まらないからである(無理やり求めようとすると、波束が一点に集中しているから振動数は無限大になり、$E=hν$に従い粒子のエネルギーは無限大になる、ということになるのだろうか)。とにかく、物質波を表す波束は、初期状態からある程度の広がりを持っている必要がある。

参考:デルタ関数と使用例

以上のことをまとめて考えると、初期状態の波束の広がりが、物質波の最小の広がりとなることがわかる。では、その最小の広がりとは具体的にどの程度なのだろうか。実はこの最小の広がりを表す式が、不確定性原理と呼ばれるものなのである。

不確定性原理の式の意味とは

不確定性原理とは、具体的には次の式で表される。

$$Δx･Δp \geq \frac{ℏ}{2}$$

この式は、正確な位置と運動量は同時に求まらないことを表す。例えば、観測によって粒子の位置が正確に求まったとする。この場合の位置の分散は$Δx=0$となる。ところが、不確定性原理の式によると$Δx･Δp$は必ず$ℏ/2$以上にならなければいけないため、$Δp$は求まらないことになる。したがって、位置$x$が正確に求まると、運動量$p$が求められなくなるといえる。逆に運動量が正確に観測できると、今度は位置が求められなくなる。

この式を導出するには、位置空間と運動量空間における粒子のゆらぎ$Δx,Δp$をそれぞれ計算すれば良い。では、これから実際に導出する。

不確定性原理による最小のばらつき

導出の方針

波動関数$ψ(x)$が持つ位置と運動量のばらつき$Δx$,$Δp$を求める。今回は粒子の存在確率が、位置空間と運動量空間上においてガウス関数（正規分布）と呼ばれる形をしていると仮定する。

今、波動関数は次の分布に従うと仮定する。

$$ψ(x)=\frac{1}{ (2πσ^2)^{\frac{1}{4}}}e^{-\frac{x^2}{4σ^2}}$$

この波動関数の絶対値の2乗(粒子の存在確率)は、有名なガウス関数の式

$$f(x)=\frac{1}{\sqrt{2πσ^2}}e^{-\frac{x^2}{2σ^2}}$$

となっている。また、この波束は、

$$\int_{-\infty}^{\infty} |ψ(x)|^2dx=\int_{-\infty}^{\infty} ψ^*(x)ψ(x)dx=1$$

になるように規格化されている(後述)。つまり、位置全体で積分すると、粒子の存在確率が1になるように規格化されているということである。

これを踏まえて、この式に従う位置と運動量のばらつきを求める。

波動関数の規格化

波動関数

$$ψ(x)=Ce^{-\frac{x^2}{4σ^2}}$$

を規格化して、先ほど仮定した波動関数がきちんと規格化されていることを確認する。

\begin{eqnarray} 1&=&\int_{-∞}^∞ |ψ(x)|^2 dx \\&=&\int_{-∞}^∞ ψ^*(x) ψ(x) dx \\&=&\int_{-∞}^{∞} Ce^{-\frac{x^2}{4σ^2}}･Ce^{-\frac{x^2}{4σ^2}} dx\\&=&C^2\int_{-∞}^{∞} e^{-\frac{x^2}{2σ^2}} dx\\&=&C^2\sqrt{2πσ^2} \end{eqnarray}

よって、波動関数の規格化定数は$C=\left(2πσ^2\right)^{-\frac{1}{4}}$となる。途中でガウス積分$\int_{-∞}^{∞} e^{-ax^2} dx=\sqrt{\frac{π}{a}}$を使った。このガウス積分はこの後も何回か出てくる。

位置のばらつきを求める

規格化が確認できたところで、いよいよ位置のばらつき$Δx$を求める。

位置のばらつきを$Δx≡\sqrt{<x^2>-<x>^2}$と定義すると、これを求めるには$<x^2>$と$<x>$がわかればよい。ここで、カッコ$<>$とは、カッコ内の物理量の期待値を表す。

また、これから出てくる$<ψ|$や$|ψ>$をまとめてブラ・ケットベクトルとよぶ。これらについて詳しくは別記事を参照してください。なぜ下の変形で積分が出てくるのかもわかります。

ブラケットベクトルを使うと、位置$x$とその２乗$x^2$の期待値$<x>,<x^2>$はそれぞれ次のように求まる。

参考:ブラベクトル・ケットベクトルの意味とは

\begin{eqnarray} <x>&=&<ψ|x|ψ>\\&=&\int_{-∞}^{∞} ψ^*xψ dx \\&=&\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} xe^{-\frac{x^2}{2σ^2}} dx \end{eqnarray}

ここで、$x$は奇関数、$e^{-\frac{x^2}{σ^2}}$は偶関数である。よって、(奇関数)×(偶関数)=(奇関数)より、被積分関数$xe^{-\frac{x^2}{σ^2}}$は奇関数である。奇関数を$-∞$から$∞$で積分すると$0$になるから、$<x>=0$が判明する。

\begin{eqnarray} <x^2>&=&<ψ|x^2|ψ>\\&=&\int_{-∞}^{∞} ψ^*x^2ψ dx \\&=&\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} x^2e^{-\frac{x^2}{2σ^2}} dx\\&=&\frac{1}{\sqrt{2πσ^2}}\frac{2σ^2\sqrt{2σ^2}\sqrt{π}}{2}\\&=&σ^2 \end{eqnarray}

途中でガウス積分$\int_{-∞}^{∞} x^2e^{-ax^2} dx=\frac{\sqrt{π}}{2a\sqrt{a}}$を使った。

以上のことから、位置のばらつき$Δx$が求められるようになる。

\begin{eqnarray} Δx&≡&\sqrt{<x^2>-<x>^2}\\&=&\sqrt{σ^2-0^2} \\&=&σ \end{eqnarray}

運動量のばらつきを求める

次に、運動量のばらつき$Δp$を求める。$Δx$のときとほとんど同じ計算である。

\begin{eqnarray} <p>&=&<ψ|\hat{p}|ψ>\\&=&\int_{-∞}^{∞} ψ^*\hat{p}ψ dx \\&=&\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} e^{-\frac{x^2}{4σ^2}}\left(-iħ\frac{d}{dx} e^{-\frac{x^2}{4σ^2}}\right) dx\\&=&\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} e^{-\frac{x^2}{4σ^2}}･(-iħ)･\left(-\frac{2}{4σ^2}xe^{-\frac{x^2}{4σ^2}}\right) dx\\&=&\frac{1}{\sqrt{2πσ^2}}\frac{iħ}{2σ^2}\int_{-∞}^{∞} xe^{-\frac{x^2}{2σ^2}} dx\\&=&\frac{1}{\sqrt{2πσ^2}}\frac{iħ}{2σ^2}･0\\&=&0 \end{eqnarray}

\begin{eqnarray} <p^2>&=&<ψ|\hat{p}^2|ψ>\\&=&\int_{-∞}^{∞} ψ^*\hat{p}^2ψ dx \\&=&\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} e^{-\frac{x^2}{4σ^2}}\left(-iħ\frac{d}{dx} \right)^2e^{-\frac{x^2}{4σ^2}} dx\\&=&\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} e^{-\frac{x^2}{4σ^2}}･(-iħ)^2･\frac{d}{dx}\left(-\frac{1}{2σ^2}xe^{-\frac{x^2}{4σ^2}}\right) dx\\&=&-\frac{(iħ)^2}{2σ^2}\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} e^{-\frac{x^2}{4σ^2}}･\frac{d}{dx}\left(xe^{-\frac{x^2}{4σ^2}}\right) dx\\&=&\frac{ħ^2}{2σ^2}\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} e^{-\frac{x^2}{4σ^2}}･\left[e^{-\frac{x^2}{4σ^2}}+x･\left(-\frac{1}{2σ^2}xe^{-\frac{x^2}{4σ^2}}\right)\right] dx\\&=&\frac{ħ^2}{2σ^2}\frac{1}{\sqrt{2πσ^2}}\int_{-∞}^{∞} \left(e^{-\frac{x^2}{2σ^2}}-\frac{x^2}{2σ^2}e^{-\frac{x^2}{2σ^2}}\right) dx\\&=&\frac{ħ^2}{2σ^2}\frac{1}{\sqrt{2πσ^2}}\left( \int_{-∞}^{∞} e^{-\frac{x^2}{2σ^2}} dx-\frac{1}{2σ^2}\int_{-∞}^{∞}x^2e^{-\frac{x^2}{2σ^2}} dx \right)\\&=&\frac{ħ^2}{2σ^2}\frac{1}{\sqrt{2πσ^2}}\left( \sqrt{2πσ^2}-\frac{1}{2σ^2}･\frac{2σ^2\sqrt{2σ^2}\sqrt{π}}{2} \right)\\&=&\frac{ħ^2}{2σ^2}\left( 1-\frac{1}{2} \right)\\&=&\frac{ħ^2}{4σ^2} \end{eqnarray}
\begin{eqnarray} Δp&≡&\sqrt{<p^2>-<p>^2}\\&=&\sqrt{\frac{ħ^2}{4σ^2}-0^2} \\&=&\frac{ħ}{2σ} \end{eqnarray}

$Δx･Δp=\frac{ħ}{2}$となるが、これはハイゼンベルグの不確定性原理$Δx･Δp\geq\frac{ħ}{2}$の等式部分となっている。

以上で、ガウス関数に従う物質波の波束は、最低でも広がり$Δx･Δp=\frac{ħ}{2}$をもつことがわかった。

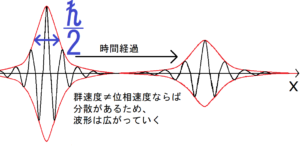
また、シュレディンガー方程式に従う波動関数が分散を持ち、時間経過で広がっていくことは前にも記事にした。このことも含めて考えると、物質波がこの最低限の広がり$Δx･Δp=\frac{ħ}{2}$から、徐々に物質波の分散によって波束が広がっていくことになる。

参考:波束と分散について

不等式を用いた不確定性原理の導出

ここまでは物質波がガウス関数に従うことを前提として考えて、物質波の広がりの最低値を求めた。だが、それが最低値だという根拠は、物質波は波束の分散により広がっていくからというものだけであり、根拠としてはやや弱いように思える。そこで、これから別の方法で、不等式を含む不確定性原理

$$Δx･Δp \geq \frac{ħ}{2}$$

を導出する。

不等式を用いた不確定性原理の証明

絶対値は常に0または正の値をとるため、任意の実数$t$で常に次の式が成立する。

$$\int_{-\infty}^{\infty} \left| tħ\frac{dφ(x)}{dx}+xφ(x) \right| ^2 dx \geq 0$$

この式の左辺を次のように変形させる。ただし、$φ^*(x)$は、波動関数$φ(x)$の複素共役である。

\begin{eqnarray}(左辺)&=&\int_{-\infty}^{\infty} \left( tħ\frac{dφ^*(x)}{dx}+xφ^*(x) \right) \left( tħ\frac{dφ(x)}{dx}+xφ(x) \right) dx\\&=&\int_{-\infty}^{\infty} t^2ħ^2\frac{dφ^*(x)}{dx}\frac{dφ(x)}{dx} dx+\int_{-\infty}^{\infty} xtħ\frac{dφ^*(x)}{dx}φ(x) dx\\&& \qquad +\int_{-\infty}^{\infty} xtħφ^*(x)\frac{dφ(x)}{dx}dx+\int_{-\infty}^{\infty} x^2φ^*(x)φ(x) dx\end{eqnarray}

以降、それぞれの項について考える。

第一項の積分

部分積分を使って第一項の積分を変形させる。

\begin{eqnarray}(第一項)&=&\int_{-\infty}^{\infty} t^2ħ^2\frac{dφ^*(x)}{dx}\frac{dφ(x)}{dx} dx\\&=&t^2ħ^2\left[φ^*(x)\frac{dφ(x)}{dx}\right]_{-\infty}^{\infty}-t^2ħ^2\int φ^*(x) \frac{d^2φ(x)}{dx^2} dx\\&=&t^2\int φ^*(x) \left( -ħ^2\frac{d^2φ(x)}{dx^2}\right) dx\\&=&t^2\int φ^*(x) \left( -iħ\frac{d}{dx}\right)^2φ(x) \ dx\\&=&t^2\int φ^*(x) \hat{p}^2 φ(x) \ dx\\&=&t^2<p^2>\\&=&t^2(<p^2>-0)\\&=&t^2(<p^2>-<p>^2)\\&=&t^2(Δp)^2\end{eqnarray}

途中で運動量演算子$\hat{p}$が代入されていることに注意すること。

参考:シュレディンガー方程式と運動量演算子の求め方

また、物質波は波束の形をしていると仮定すると、無限遠($-\infty$と$+\infty$)には物質波は存在しないことになる。そのため、途中の

$$\left[φ^*(x)\frac{dφ(x)}{dx}\right]_{-\infty}^{\infty}$$

は0になることにも注意する。

第二項・第三項の積分

第二項と第三項の積分はまとめて考える。

\begin{eqnarray}(第二項)+(第三項)&=&tħ\int_{-\infty}^{\infty} x\left( \frac{dφ^*(x)}{dx}φ(x) +φ^*(x)\frac{dφ(x)}{dx}\right) dx\\&=&tħ\int_{-\infty}^{\infty} x\left( \frac{d}{dx}[φ^*(x)φ(x)]\right) dx\\&=&tħ\int_{-\infty}^{\infty} x\left( \frac{d|φ(x)|^2}{dx}\right) dx\\&=&tħ \left( \left[x|φ(x)|^2\right]_{-\infty}^{\infty} -\int_{-\infty}^{\infty} |φ(x)|^2 dx \right)\\&=&tħ \left( 0-1 \right)\\&=&-tħ \end{eqnarray}

まず、$\left[x|φ(x)|^2\right]_{-\infty}^{\infty}$は第一項のときと同じ理由で0である。

また、

$$\int_{-\infty}^{\infty} |φ(x)|^2 dx=1$$

は波動関数の規格化条件である。

第四項の積分

第四項の積分は明らかに位置の2乗の期待値$<x^2>$の式と同じである。

\begin{eqnarray}\int_{-\infty}^{\infty} φ^*(x)x^2φ(x) dx&=&<x^2>\\&=&<x^2>-<x>^2\\&=&(Δx)^2\end{eqnarray}

これまでの積分のまとめ

以上の積分を最初の不等式に代入する。

$$t^2(Δp)^2-tħ+(Δx)^2 \geq 0$$

この式を変数$t$の2次不等式と考える。この不等式を満たすような判別式は

$$ħ^2-4(Δp)^2(Δx)^2 \leq 0$$

だから、これを変形して不確定性原理の式

$$(Δp)^2(Δx)^2 \geq \frac{ħ^2}{4}$$

を得る。

まとめ

・不確定性原理とは、粒子の位置と運動量を同時に観測することはできないことである。位置を正確に測定できたら正確な運動量が求められなくなり、逆に運動量が正確に測定できたら粒子の正確な位置が求められなくなる。

・今回は、物質波がガウス関数の形をしていることを前提としたときの期待値からと、絶対値を含む不等式からの2通りで、不確定性原理の導出を行った。

参考文献

・中嶋貞雄(1984)『量子力学II』,岩波書店.

・原田勲･杉山忠男(2009)『講談社基礎物理学シリーズ6 量子力学I』,講談社.

・村上雅人(2006)『なるほど量子力学II』,海鳴社.

不確定性原理の概要と導出

不確定性原理とは

物質波と波束の分散について

物質波の最小の分散とは

不確定性原理の式の意味とは

不確定性原理による最小のばらつき

導出の方針

波動関数の規格化

位置のばらつきを求める

運動量のばらつきを求める

不等式を用いた不確定性原理の導出

不等式を用いた不確定性原理の証明

第一項の積分

第二項・第三項の積分

第四項の積分

これまでの積分のまとめ

まとめ

参考文献

コメントを残すコメントをキャンセル

おすすめ記事

twitter

カテゴリー

不確定性原理とは

物質波と波束の分散について

物質波の最小の分散とは

不確定性原理の式の意味とは

不確定性原理による最小のばらつき

導出の方針

波動関数の規格化

位置のばらつきを求める

運動量のばらつきを求める

不等式を用いた不確定性原理の導出

不等式を用いた不確定性原理の証明

第一項の積分

第二項・第三項の積分

第四項の積分

これまでの積分のまとめ

まとめ

参考文献

関連記事(広告含む)

SNSでもご購読できます。

コメントを残す コメントをキャンセル

おすすめ記事

twitter

カテゴリー

コメントを残すコメントをキャンセル