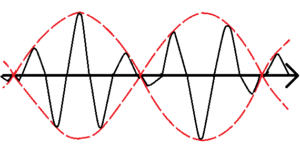
上図は、2種類の波が重なり合ってうなりが発生している様子を表している。波の振幅を赤い点線で結んだが、群速度\(v_g\)とは、この赤線で表した波が動く速度を表したものである。このことから、群速度はうなりの構造の速度とよく言われる。
$$v_g≡\frac{dω}{dk}$$
一方、黒い実線の波の速さは位相速度\(v_φ\)と呼ぶ。
$$v_φ≡\frac{\bar{ω}}{\bar{k}}$$
目次
群速度と位相速度の導出
合成波の求め方
次の二つの波の重ね合わせを考える。
$$u_1(x,t)=Acos(k_1x-ω_1t)$$$$u_2(x,t)=Acos(k_2x-ω_2t)$$
重ね合わせの定理より、合成波\(u(x,t)\)は2つの波の和となる。
ここで、2つの波の波数と角振動数の平均値をそれぞれ\(\bar{k}\)、\(\bar{ω}\)、差をそれぞれ\(Δk\)、\(Δω\)とおいた。途中で次の三角関数の公式が使われていることに注意する。
合成波の式の考察
以上から、合成波の式が求められた。
この式から合成波は、cos波\(2Acos\left(\bar{k}x-\bar{ω}t \right)\)と因子\(cos\left( \frac{Δkx-Δωt}{2} \right)\)の積で求められることがわかる。では、それぞれについて詳しく見ていこう。
以降、両方の波の波数と角振動数の差が小さいとする。つまり、\(Δk<<k_1,k_2\)、\(Δω<<ω_1,ω_2\)である。
\(cos\left( \frac{Δkx-Δωt}{2} \right)\)と群速度
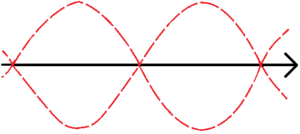
まず因子\(cos\left( \frac{Δkx-Δωt}{2} \right)\)について考える。
\(Δk<<k_1,k_2\)より、\(x\)の変動による位相の変化は小さい。したがって、波長が長いことがわかる。同様にして、\(Δω<<ω_1,ω_2\)より、波の速さも遅くなる。つまり、この部分は上図でいう赤線の波を表している。
また、この因子は次のように変形できる。
この因子の\(t\)の係数\(Δω/Δk\)が赤い波の速度となる。これの微小量をとることで、群速度\(v_g\)が求められる。
$$v_g=\frac{dω}{dk}$$
\(2A\left(\bar{k}x-\bar{ω}t \right)\)と位相速度
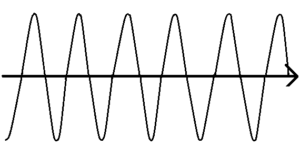
この因子は、振幅が\(2A\)のcos波を表している。位相速度はこの黒線の波の速度のことを指すが、この位相速度も群速度と同じ考え方で、次のように求まる。
$$v_φ≡\frac{\bar{ω}}{\bar{k}}$$
\(Δk<<k_1,k_2\)と\(Δω<<ω_1,ω_2\)より、黒線の波は、赤線の波より波長も短く、波の速度も速いことがわかる。
まとめ
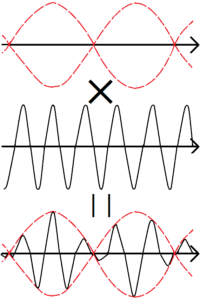
・2つの波が合成されたとき、合成波は次の数式で表された。
・群速度\(v_g\)は次のように定義される。
$$v_g≡\frac{dω}{dk}$$
$$v_φ≡\frac{\bar{ω}}{\bar{k}}$$
参考文献
・長谷川修司(2009)『振動・波動 (講談社基礎物理学シリーズ)』,講談社.

