調和振動子とは、単振動をする系のことである。
$$f=-kx$$
調和振動子のポテンシャルエネルギーは、次のように与えられる。
$$V(x)=\frac{1}{2}mω^2x^2$$
単振動の復習
簡単に単振動の復習をする。
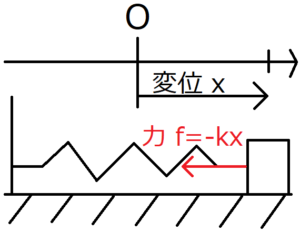
ばねのつり合いの位置を原点とする。時刻\(t=0\)に位置\(x_0\)で手を離すと、物体の軌跡\(x(t)\)と角速度\(ω\)は次のように表される。
$$x(t)=x_0cosωt$$
$$ω=\sqrt{\frac{k}{m}}$$
参考:単振動する物体の軌跡
ポテンシャルエネルギーの導出
ポテンシャルエネルギー\(V(x)\)は、力\(f(x)\)を距離で積分することで定義された。
$$V(x)=-\int f(x) dx$$
ばねの変位がxのときのポテンシャルエネルギーは、次のようにして計算される。
\(ω=\sqrt{\frac{k}{m}}\)を\(k\)について解くと、
$$k=mω^2$$
後はこの\(k\)をポテンシャルエネルギーに代入すればよい。
$$V(x)=\frac{1}{2}mω^2x^2$$
調和振動子のハミルトニアン
ハミルトニアン\(H\)とは、系全体が含むエネルギーのことである。今考えている系のハミルトニアンは、運動エネルギー\(T\)とポテンシャルエネルギー\(V\)の和となる。
ハミルトニアン中の運動エネルギーでは、速度\(v\)ではなく運動量\(p=mv\)を使うことが多い。
ハミルトニアンについて、詳しくは次の記事を参照のこと。下の記事では、ハミルトニアンの定義や、ハミルトニアンを運動エネルギーとポテンシャルエネルギーの和とみなせる理由が書いてある。
参考文献
・長谷川修司(2009)『講談社基礎物理学シリーズ2 振動・波動』,講談社.
・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

