[mathjax]
重心
物体の正体
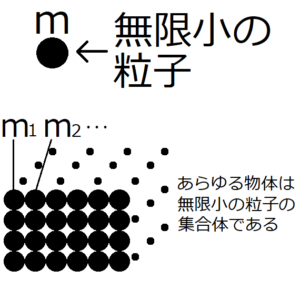
無限小の大きさの粒子が存在する。あらゆる形の物体は、この粒子の集合体とみなすことができる。一つ一つの粒子を区別して、i番目の粒子の質量を\(m_i\)とおく。そして物体が全部で\(N\)個の粒子で構成されているとすると、その物体の総質量\(M\)は次のように書ける。
そして、この粒子は、体積や角速度といった情報を持たず、質量と位置という情報のみをもつ質点として考えることができる。以降、この粒子のことを質点と表現する。
重心とは
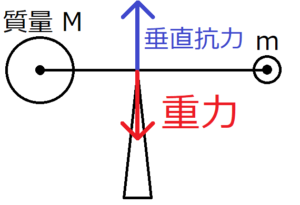
上図のような天秤を考える。ただし、棒の質量は無視する。棒の両端にはそれぞれ質量\(M,m\)の重りが取り付けてある。そしてつり合いの位置は、質量\(M\)の重りからは\(R\)、質量\(m\)の重りからは\(r\)だけ離れているとする。
この天秤は、重り付きの棒と支えの2つのパーツから成り立っている。パーツごとに考えると、棒は重力によって支えを押しているが、支えは棒を垂直抗力という形で押し返している。この状態は、棒と同じ質量の質点が、支えの上に乗っかっていると考えることもできる。
つまり、大きさのある物体の運動を考えるときは、その物体の重心の位置にあり、かつその物体と同じ質量の質点の運動を考えればよい。
下の記事では、このことを数式を使って考察している。
参考:剛体の運動方程式
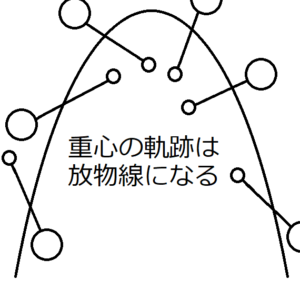
もし天秤の棒を空中に放り投げたら、その棒の重心は上図のように放物線を描くだろう。その理由は、この棒の重心の運動は、棒と同じ質量の質点の運動と同じようにみることができるからである。
重心の導出
以上で重心の意味を確認したが、次に重心の位置は一般的にどのようにして求められるか調べる。
天秤と力のモーメント
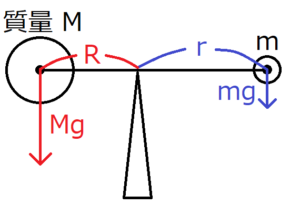
前と同じ天秤を考える。
ここで、それぞれの重りが支えを回転軸にして棒を回す力、つまり力のモーメントを考える。力のモーメントの大きさは、その定義より、次のように書ける。
ここで、上の図ではベクトル\({\bf r}\)と力\({\bf F}\)のなす角が\(90°\)であることに注意する。
参考:内積・外積の用途
したがって、つり合いの位置から\(R\)だけ離れた質量\(M\)の重りが、棒を反時計回りに回す力のモーメントの大きさ\(N_M\)は、\(N_M=MgR\)となる。
同様にして、質量\(m\)の力のモーメント\(N_m\)は、時計回りに回す力のモーメントを負とすると、\(N_m=-mgr\)となる。
棒が回転しないということは、この2つのモーメントがつり合っていることを意味する。
右辺の第二項を移項して、両辺を\(g\)で割る。
位置ベクトルを使った重心の表現
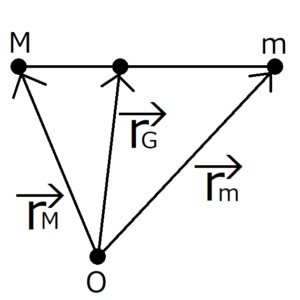
棒の重心の位置ベクトルを\({\bf r}_G\)、質量\(M\)の重りの位置ベクトルを\({\bf r}_M\)、質量\(m\)の重りの位置ベクトルを\({\bf r}_m\)とおく。すると、式(1)は次のように書き換えられる。
この式を\({\bf r}_G\)で解く。
これで、位置ベクトルを使って棒の重心を求められた。
多くの質点の重心
ここまでは2つの質点の重心を考えたが、\(N\)個の質点の重心も同様にして求められる。i番目の質点が位置\({\bf r}_i\)にあり、その質量を\(m_i\)とする。
これで、一般的な重心の式が求められた。
まとめ
・重心を求める式を、天秤を使って求めた。
参考文献
・都築嘉弘(2005)『チャート式シリーズ 新物理II』,数研出版.
・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

