なぜ音波は波動方程式に従うのか

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

身近な波動の例として、音波が挙げられる。音波とは、空気の振動によって伝わる波のことで、縦波である。前に弦の振動から波動方程式を求めることを別記事でしたが、こちらは縦波なので別に考える必要がある。

この記事では、なぜ縦波である音波も波動方程式に従うのかを考える。

1 なぜ音波は縦波か
2 音波が波動方程式に従う理由
3 音速について
4 まとめ
5 参考文献

なぜ音波は縦波か

本題に入る前に、なぜ音波が縦波であるかを解説する。

そもそも横波とは、波を伝える媒質が、進行方向に対して垂直方向に曲がるような波のことである。そして、媒質の弾性力によって、曲げられた状態から元に戻ろうとすることで、横波は伝搬される。

したがって、音波が横波であるためには、その媒質である空気に曲げに対する弾性力がなければならない。ところが、空気を曲げてもそれに反発するような力は働かないため、空気には横波を伝える能力がないといえる。よって、空気を媒質とする音波は横波にはなりえない。

一方、音波を縦波として考えたらどうなるか。縦波の伝搬とは、媒質が進行方向と同じ向きで振動することで、媒質の疎密が伝わることである。そして、媒質の疎密が波として伝わるには、媒質自身が圧縮に対して膨張しようとする能力を持っている必要がある。空気は圧縮されると、それに反発して膨張しようとする力をつくる。このように、圧縮に対する弾性力が空気にはあるため、空気は縦波を伝えることができる。したがって、音波は縦波である。

音波が波動方程式に従う理由

音波が縦波であることを考察できたので、本題に入る。

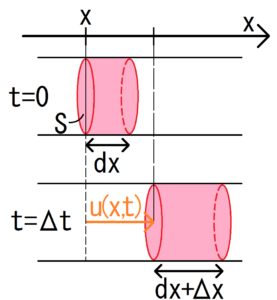
上の図のような、断面積Sの円筒中に伝わる音波について考える。この円筒中の、長さ$Δx$の円柱に含まれる空気の塊に注目する。

円柱にかかる圧力$p$

運動方程式

面積$S$の面に圧力$p$がかかっている場合、その面に働く力$F$は次のように表せた。

$$F=pS$$

この関係をもとに、円柱形の空気の塊に働く力の運動方程式を組み立てる。ただし、空気の塊の左端の変位を$u(x,t)$とした。

$$m\frac{\partial ^2u}{\partial t^2}=pS$$

空気の密度を$ρ$とすると、この円柱の体積は$SΔx$だから、その空気の塊の質量$m$は

$$m=ρSΔx$$

となる。これを運動方程式に代入する。

$$ρSΔx\frac{\partial ^2u}{\partial t^2}=pS$$

空気の塊にかかる圧力について

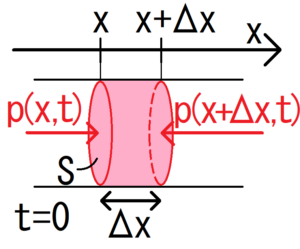
音波がなく、円筒中の空気密度が一様になっている状態での空気の圧力を$p_0$とおく。この状態の円筒に縦波である音波を侵入させると、当然円筒中の圧力も変化する。このときの圧力の変化分を$Δp(x,t)$とおく。音波が侵入している状態ではもはや円筒中の空気の密度は一様ではなく、また時間によって空気密度は絶えず変化するようになるため、$Δp$は位置$x$と時刻$t$に依存する。したがって、時刻$t$で位置$x$にかかる圧力の大きさ$p(x,t)$は、

$$p(x,t)=p_0+Δp(x,t)$$

また、今注目している円柱状の空気の塊の左側からはたらく圧力$p(x,t)$はx軸方向に働き、円柱の右側からはたらく圧力$p(x+Δx,t)$はx軸の逆方向に働く。このことから円柱に働く総圧力は、

$$p_{総圧力}=p(x,t)-p(x+Δx,t)$$

となる。x軸とは逆向きだから、$p(x+Δx,t)$にはマイナスがつく。

以上までの空気の質量と圧力の式を、運動方程式に代入する。

$$ρSΔx\frac{\partial ^2 u}{\partial t^2}=-(Δp(x+Δx,t)-Δp(x,t))S$$

両辺を断面積$S$と円柱の長さ$Δx$で割る。

$$ρ\frac{\partial ^2u}{\partial t^2}=-\frac{Δp(x+Δx,t)-Δp(x,t)}{Δx}$$

右辺の$Δx$の極限$Δx \to 0$をとった後、$lim$を使った微分の定義

$$\frac{df(a)}{dx}=\displaystyle \lim_{h \to 0} \frac{f(a+h)-f(a)}{h}$$

を、上の運動方程式に適応させる。

$$ρ\frac{\partial ^2 u}{\partial t^2}=-\frac{\partial Δp(x,t)}{\partial x}･･･(1)$$

これで、変位$u(x,t)$と圧力$Δp(x,t)$の関係式が求められた。この式は後々使うことになる。

波動方程式とは変位$u(x,t)$に関する偏微分方程式だから、式(1)の右辺の圧力$Δp$を変位$u(x,t)$で表せたら良さそうだ。

体積弾性率

気体は、周囲の圧力$p$が大きくなるにつれて体積が縮んでいく。この体積の縮み方に関するパラメータとして、体積弾性率$K$が次のように定義できる。ただし、元々の気体の体積を$V$とおくことにする。

$$K≡-V\frac{∂p}{∂V}$$

参考:熱力学における圧縮率・体積弾性率・体膨張率とは

この定義式は、

$$Δp=-K\frac{ΔV}{V}$$

の微小量をとったものと考えることができる。$ΔV/V$は、元の体積$V$に対してどれだけ体積が変化したかを表す指標で、体積の相対変化量とよばれる。

この式を、今考えている円柱形の空気の塊の膨張・圧縮に適応させてみる。円柱の左端の変位が$u(x)$、右端の変位が$u(x+Δx)$となるため、円柱の体積は$(u(x+Δx)-u(x))S$となる。空気の塊の元の体積は$SΔx$だから、これらを上の式に代入すると、$Δp$が求まる。

\begin{eqnarray}Δp&=&-K\frac{ΔV}{V}\\&=&-K\frac{(u(x+Δx)-u(x))S}{SΔx}\\&=&-K\frac{u(x+Δx)-u(x)}{Δx}\end{eqnarray}

極限$Δx \to 0$をとると

$$\lim_{Δx \to 0}Δp=-K\frac{\partial u}{\partial x}･･･(2)$$

波動方程式の導出

式(1)に式(2)を代入する。

\begin{eqnarray}ρ\frac{\partial ^2u}{\partial t^2}&=&-\frac{\partial Δp(x,t)}{\partial x}\\&=&-\frac{\partial }{\partial x}\left( -K\frac{\partial u}{\partial x} \right) \\&=&K\frac{\partial ^2u}{\partial x^2} \end{eqnarray}

これの両辺を$ρ$で割る。

$$\frac{\partial ^2u}{\partial t^2}=\frac{K}{ρ}\frac{\partial ^2u}{\partial x^2}$$

$c^2≡\frac{K}{ρ}$とおくと、

$$\frac{\partial ^2u}{\partial t^2}=c^2\frac{\partial ^2u}{\partial x^2}$$

以上で、波動方程式の導出が完了した。$c$は速さの次元を持ち、音速を表している。

ちなみに、波動方程式に従う波は群速度と位相速度が等しく、分散がない。そのため、長距離伝搬しても波形は維持される。この性質によって、伝搬距離によって音の高さが変わることはない。

参考:波束と分散について

音速について

音速$c$が満たす式はわかったが、これをもう少し変形させてみる。

先程までは空気の塊の伸縮を考えてきたが、この伸縮を断熱過程と仮定する。断熱過程では、次の関係が成り立つ。

$$pV^γ=C(定数)･･･(3)$$

ただし、$γ$は比熱比といい、1molあたりの定圧熱容量$C_p$と定積熱容量$C_V$の比で定義される。

$$γ≡\frac{C_p}{C_V}$$

参考:理想気体と過程に関わる公式集

式(3)をpについて解いて、それを体積弾性率の式に代入する。

\begin{eqnarray}K&≡&-V\frac{∂p}{∂V}\\&=&-V\frac{∂}{∂V} \left( CV^{-γ}\right)\\&=&-V \left( -γCV^{-γ-1}\right)\\&=&V \left( γCV^{-γ-1}\right)\\&=& γCV^{-γ}\\&=& γP\end{eqnarray}

これを、$c^2$の定義式に代入する。

\begin{eqnarray}c&≡&\sqrt{\frac{K}{ρ}}\\&=&\sqrt{\frac{γP}{ρ}}\\&=&\sqrt{\frac{γPV}{ρV}}\\&=&\sqrt{\frac{γnRT}{M}}\end{eqnarray}

ここで、$M$とは空気の質量である。

では、これから具体的な値を代入して、体積$1m^3$中の常温下での音速を求めてみる。

まず、空気の密度は$ρ=1.293kg/m^3$であった。また、常温27℃の絶対温度は300Kである。

1molの気体の容積は22.4L(0.0224m^3)であるため、1m^3(1000L)に含まれる気体のmol数nは、

$$n=\frac{1000[L]}{22.4}≒44.6[mol]$$

となる。空気の比熱比を$γ≒1.40$とすると、

\begin{eqnarray}c&=&\sqrt{\frac{γnRT}{M}}\\&=&\sqrt{\frac{1.40･44.6･8.31･300}{1.293}}\\&=&\sqrt{\frac{1.40･44.6･8.31･300}{1.293}}≒347[m/s]\end{eqnarray}

一般的な音速は340.29m/sとされているため、おおよそこの値に一致する。

まとめ

・音波が縦波で、波動方程式に従うことを示した。

・常温下での音速を求めた。

参考文献

・長谷川修司(2009)『講談社基礎物理学シリーズ2 振動・波動』,講談社.

なぜ音波は波動方程式に従うのか

なぜ音波は縦波か

音波が波動方程式に従う理由