剛体の運動方程式

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

[mathjax]

力を加えても変形しない物体を剛体という。そして、剛体は質点の集合体とみなすことができる。この記事では、剛体の運動方程式を導出してみる。

$\displaystyle M\frac{d^2{\bf r}_G}{dt^2}=\sum_{i=1}^N {\bf F}_i$

目次 [hide]

1 j番目の質点の運動方程式
- 1.1 質点同士の相互作用と内力
- 1.2 外力と運動方程式
2 質点系全体の運動方程式
- 2.1 内力の総和
- 2.2 質点系全体の運動方程式
3 重心を使った運動方程式
4 剛体の回転運動について
5 まとめ
6 参考文献

j番目の質点の運動方程式

質点同士の相互作用と内力

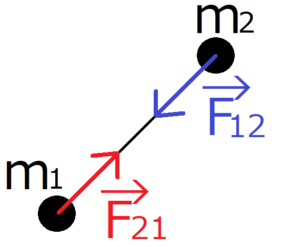
上図のように、2つの質点の間には力が働いている。質点 $m_1$ が $m_2$ に及ぼしている力を ${\bf F}_{12}$ 、逆に質点 $m_2$ が $m_1$ に及ぼしている力を ${\bf F}_{21}$ とおく。作用反作用の法則より、次の関係が成り立つ。

${\bf F}_{12}=-{\bf F}_{21}$

したがって、もし質点が全部で $N$ あったら、質点 $m_1$ が受ける相互作用の力の和は、次のように表される。

$\displaystyle {\bf F}_{21}+{\bf F}_{31}+\cdots+{\bf F}_{N1}=\sum_{i=2}^N {\bf F}_{i1}$

この式を、 $j$ 番目の質点 $m_j$ が受ける相互作用の力に書き換えると、次のようになる。ただし、質点 $m_j$ は自分自身には力を及ぼさないから、 ${\bf F}_{jj}=0$ となることに注意する。

$\displaystyle \sum_{i=1(i≠j)}^N {\bf F}_{ij}$

質点 $N$ 個の塊を一つの質点系と考えると、今まで考えてきた相互作用の力は、質点系の内部で作用していることになる。このような力を内力とよぶ。

外力と運動方程式

一方内力と違い、質点系の外部から作用するような力を外力とよぶ。質点 $m_j$ に働く外力を ${\bf F}_j$ とおく。質点 $m_j$ にかかるすべての力は、内力と外力の和になるから、この質点 $m_j$ に関する運動方程式は次のようになる。

$\displaystyle m_j\frac{d^2{\bf r}_j}{dt^2}={\bf F}_j+\sum_{i=1(i≠j)}^N {\bf F}_{ij}$

質点 $m_j$ の運動量 ${\bf p}_j$ を使うと、次のように変形できる。

$\displaystyle \frac{d{\bf p}_j}{dt}={\bf F}_j+\sum_{i=1(i≠j)}^N {\bf F}_{ij}$

以上で、j番目の質点の運動方程式が求められた。

質点系全体の運動方程式

内力の総和

2つの質点からなる質点系において、作用反作用の法則より、 ${\bf F}_{ij}=-{\bf F}_{ji} \ (i≠j)$ になることは記事の最初に確認した。したがって、その質点系の内力の和は、次のように計算できる。

$\begin{eqnarray} {\bf F}_{ij}+{\bf F}_{ji}&=&{\bf F}_{ij}-{\bf F}_{ij}\\&=&0 \end{eqnarray}$

これを、 $N$ 個の質点からなる質点系に拡張する。質点 $m_j$ は自分自身には力を及ぼさないから ${\bf F}_{jj}=0$ になることを考慮すると、次の等式が成立する。

$\displaystyle \sum_{i=1}^N\sum_{j=1}^N {\bf F}_{ij}=0$

以上より、 $N$ 個の質点を含む質点系における内力の総和は0になる。

質点系全体の運動方程式

内力が0になることで、質点系全体に働く力は外力のみと考えることができる。

$\displaystyle \sum_{j=1}^N m_j\frac{d^2{\bf r}_j}{dt^2}=\sum_{j=1}^N {\bf F}_j･･･(1)$

系全体の総質量 $\displaystyle M=\sum_{j=1}^N m_j$ を使うと、式(1)は次のように書き直せる。

$\displaystyle M\sum_{j=1}^N \frac{d^2{\bf r}_j}{dt^2}=\sum_{j=1}^N {\bf F}_j$

また、質点 $m_j$ の運動量 ${\bf p}_j=m_j\frac{d{\bf r}_j}{dt}$ を導入すると、式(1)は次のようにも変形できる。

$\displaystyle \sum_{j=1}^N \frac{d{\bf p}_j}{dt}=\sum_{j=1}^N {\bf F}_j$

系全体の運動量 $\displaystyle {\bf P}=\sum_{j=1}^N {\bf p}_j$ も導入してみる。

$\displaystyle \frac{d{\bf P}}{dt}=\sum_{j=1}^N {\bf F}_j･･･(2)$

重心を使った運動方程式

重心 ${\bf r}_G$ は、次のような式で定義された。

${\bf r}_G=\frac{\displaystyle \sum_{i=1}^N m_i{\bf r}_i}{\displaystyle \sum_{i=1}^N m_i }$

参考:天秤から考える重心の意味と導出

この式の右辺の分母は、質量系の総質量 $M$ そのままである。

$M{\bf r}_G=\displaystyle \sum_{i=1}^N m_i{\bf r}_i$

この式をもとに、質量系全体の運動量 ${\bf P}$ の変形を考えると、

$\begin{eqnarray} \displaystyle {\bf P}&=&\sum_{j=1}^N m_j\frac{d{\bf r}_j}{dt}\\&=&\sum_{j=1}^N \frac{d}{dt}(m_j{\bf r}_j)\\&=&\frac{d}{dt} \sum_{j=1}^N (m_j{\bf r}_j)\\&=&\frac{d}{dt}(M{\bf r}_G)\\&=&M\frac{d{\bf r}_G}{dt}･･･(3) \end{eqnarray}$

この式中の $\displaystyle \sum_{j=1}^N$ は有限和だから、 $\displaystyle \sum_{j=1}^N$ と $\displaystyle \frac{d}{dt}$ の入れ替えは可能である。

後は式(2)に式(3)を代入すればよい。

$\displaystyle M\frac{d^2{\bf r}_G}{dt^2}=\sum_{j=1}^N {\bf F}_j$

この式は、複数の質点からなる質点系全体の並進運動を考えるときは、その物体の重心の位置にあり、かつ質量系全体の総質量と等しい質量をもつ質点の運動を考えればよいことを表している。

剛体の回転運動について

これまでは剛体の並進運動について考えてきた。実は剛体の回転運動についても、角運動量ベクトル ${\bf L}$ と力のモーメント ${\bf N}$ とすると、次のような関係式が成り立つ。

$\frac{d{\bf L}}{dt}={\bf N}$

参考:力のモーメントと角運動量の関係

まとめ

・ $N$ 個の質点からなる質点系の運動方程式を求めることで、剛体の運動方程式を導出した。

・剛体の運動方程式を、重心を使って書き直した。

参考文献

・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

剛体の運動方程式