ガウスの法則とは、電場\(\bf E\)と電荷密度\(ρ\)の関係式のことである。この法則は、マクスウェル方程式の一つとされるほど、電磁気学において重要なものである。
この記事では、ガウスの法則の導出を行う。
目次
立体角の導入
ガウスの法則の導出には、立体角という概念が不可欠である。なぜならば、この立体角を導入することで、あらゆる閉曲面を球面のように考えることができるようになるからだ。
球面\(S\)の立体角
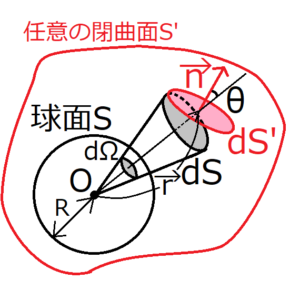
原点\(O\)を中心とする半径\(R\)の球面\(S\)が存在する。そして、原点から球面をみたときの球面の面積\(dS\)を、球の半径の2乗\(R^2\)で割ったものを、原点の中心角\(dΩ\)と定義する。
立体角の定義には通常、単位球(半径\(R=1\)の球面)を用いる。
$$dΩ=dS$$
今までよく考えてきた2直線間の角度と違って、立体角は球面の面積を使って定義されることに注意する。
立体角の例
この単位球面の面積は\(S=4π\)であるから、球の中心からみた球全体の中心角も\(dΩ=4π\)となる。
任意の閉曲面\(S’\)の立体角
球の表面の微小部分\(dS\)と、任意の閉曲面の微小部分\(dS’\)のなす角度を\(θ\)とする。ここで、上の図より\(dS=dS’cosθ\)という関係がわかる。この関係を使って、\(dS\)に関する立体角\(dΩ\)の定義式を、\(dS’\)に関する立体角\(dΩ\)に変形させる。
電場\(\bf E\)は電荷がある原点から放射状に広がるものだが、立体角を導入することで、任意の閉曲面\(S’\)から垂直に出ていく電場\(\bf E\)を考えられるようになった。
点電荷\(q\)が閉曲面\(S’\)に含まれる場合
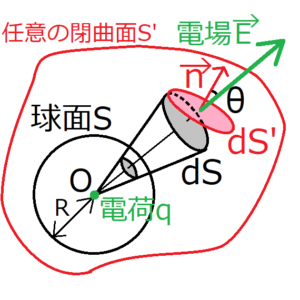
電場とは、電荷がつくる場のことを指す。
この電場の定義式の両辺を、任意の閉曲面\(S’\)で面積分する。
球の中心から見た球面全体の立体角は\(4π\)だから、立体角\(dΩ\)を球面\(S\)全体で面積分すると\(4π\)となる。
この式は、任意の閉曲面\(S’\)が点電荷\(q\)を含むとき、閉曲面\(S’\)を垂直に通過する電場\(\bf E\)を閉曲面\(S’\)上で面積分すると、\(q/ε_0\)という定数になることを意味する。
面積分についての補足
上の面積分で導入していた\(d{\bf S}’\)とは、大きさが微小面積\(dS’\)で、かつ方向がその微小面積に対して垂直であるようなベクトルのことを指す。この\(d{\bf S}’\)は、微小面積\(dS’\)に垂直かつ大きさが1である法線ベクトル\(\bf n\)を使って次のように書ける。
つまり、内積\({\bf E}・d{\bf S}’\)とは、微小面積\(dS’\)に対して垂直に通過する電場の大きさを表している。したがって、これを閉曲面\(S’\)全体で積分することで、閉曲面\(S’\)を垂直に通過する電場の大きさの総和を求めることができる。
点電荷\(q\)が閉曲面\(S’\)に含まれない場合
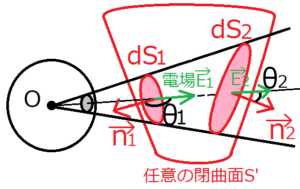
先ほどは閉曲面\(S’\)中に点電荷\(q\)が含まれる場合を考えたが、今回は含まれない場合を考える。上の図の原点\(O\)に、電荷\(q\)が存在する場合を考える。この場合、電場が閉曲面\(S’\)に入る場所と、電場が\(S’\)から出る場所が存在する。それぞれにおける電場と微小面積の内積\({\bf E}・d{\bf S}\)を、前と同様にして求める。電場\({\bf E}_1\)が閉曲面\(S’\)に入ってくる微小面積を\(d{\bf S}_1\)、電場\({\bf E}_2\)が閉曲面\(S’\)から出ていく微小面積を\(d{\bf S}_2\)とおく。また、\(d{\bf S}_1\)と電場の通り道がなす最小の角度は\((π-θ_1)\)となっていることに注意する。
以上より、
このことから、点電荷\(q\)が閉曲面\(S’\)に含まれない場合、\({\bf E}・d{\bf S}\)の面積分は0になる。
閉曲面に複数の点電荷が含まれる場合
次に、閉曲面\(S’\)中に複数の電荷が含まれている場合を考える。今、閉曲面\(S’\)中にn個の電荷が含まれており、i番目の電荷の電荷量を\(q_i\)と表す。そして、閉曲面\(S’\)に含まれる電荷の総和を\(Q\)とする。
また、i番目の電荷がつくる電場を\({\bf E}_i\)とすると、閉曲面\(S’\)中のすべての電荷がつくる電場の総和\({\bf E}\)は、次のように書ける。
それぞれの電荷\(q_i\)と電場\({\bf E}_i\)においても式(1)が成立するから、
この式(4)に、式(2)と式(3)を適応させる。
電荷密度\(ρ\)を使用した場合
任意の閉曲面\(S’\)中の電荷\(Q\)は、電荷密度\(ρ({\bf r})\)を閉曲面\(S’\)中で体積積分したもので表される。この閉曲面\(S’\)で囲まれた体積を\(V\)とおくと、
この式の\(Q\)を、式(5)の電荷\(Q\)に代入すると、
この式が、ガウスの法則の積分形である。
まとめ
・任意の閉曲面\(S’\)内に電荷\(Q\)が存在する場合、電場\(\bf E\)と電荷\(Q\)の間に次の関係が成り立つ。
・任意の閉曲面\(S’\)内に電荷が全く存在しない場合、電場\(\bf E\)の面積分は0になる。
参考文献
・伊東敏雄(2008)『電磁気学 (朝倉物理学選書)』,朝倉書店.
・砂川重信(1987)『電磁気学 (物理テキストシリーズ 4)』,岩波書店.
・砂川重信(1988)『電磁気学―初めて学ぶ人のために』,培風館.

