複素積分における積分経路の設定方法

重要なお知らせあなたのWebブラウザーでJavaScriptを有効にする方法

この前は定理によって複素積分を求める方法について記事にしたが、単純に定理にあてはめるだけでは解けない複素積分も存在する。ところが、そのような複素積分でも、自分で積分経路を設定することで解けるようになる。さらに、実数関数の積分を複素積分に拡張して解くこともできる。今回はこれを適用して解ける問題を見てみる。

目次 [hide]

1 特異点を避けて積分範囲を設定する
例題 $sinx/x$ の積分
3 参考文献

特異点を避けて積分範囲を設定する

もし積分範囲内に正則でない点があるならば、その点を避けて積分範囲を設定する。そうすれば、コーシーの積分定理(積分範囲内がすべて正則なら複素積分の値は0)より、求めたい積分を簡単に計算できる。もしコーシーの積分定理を知らない場合は、まず下の記事から読むことをおすすめする。

リンク：定理による複素積分の解き方まとめ

早速例題を解いてみる。

例題 $sinx/x$ の積分

大学でもよく見る例題を解いてみる。

$\int_0^∞ \frac{sinx}{x} dx$

被積分関数の変形

被積分関数は $\frac{sinx}{x}$ だが、このまま積分を考えるには面倒である。そこで、 $sinx$ を変形する。

$\frac{sinx}{x}=\frac{e^{ix}-e^{-ix}}{2ix}$

この式から、 $\frac{sinx}{x}$ の積分を求めるには $\frac{e^{ix}}{x}$ を積分すればよい。

この被積分関数 $\frac{e^{ix}}{x}$ は、初等関数では積分できないと思われるため、複素積分を導入することにする。複素積分の変数は、 $x$ よりも $z$ を多く使う(実数の変数はxがよく使われるが、複素数の変数はzがよく使われるため)。だからこれ以降、積分経路に虚部が存在する場合は、被積分関数は $\frac{e^{iz}}{z}$ と表すことにする。

積分範囲の設定

この被積分関数 $\frac{e^{iz}}{z}$ は、 $z=0$ で分母が $0$ になってしまうため、積分経路は $z=0$ を避けて設定する。

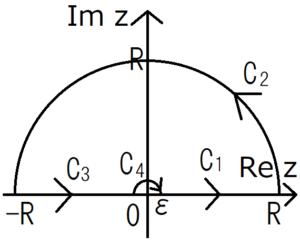
この図のような積分経路を考える。計算の都合上、最初は $R$ は有限の値としておくが、最終的に $∞$ に発散させて考える。同じく $ε$ も、最終的には $0$ に近づける。わざわざ積分範囲をループさせた理由は、コーシーの積分定理を使うためである。

コーシーの積分定理の適用

今、積分範囲 $C_1+C_2+C_3+C_4$ は、経路上やその内部に特異点を含まない。したがって、コーシーの積分定理より次の式が成り立つ。

$\int_{C_1} \frac{e^{iz}}{z} dz+\int_{C_2} \frac{e^{iz}}{z} dz+\int_{C_3} \frac{e^{iz}}{z} dz+\int_{C_4} \frac{e^{iz}}{z} dz=0$

次から、それぞれの積分経路における積分の値を吟味していく。

$C_1$ における積分

上の積分範囲を表した図より、 $C_1$ での積分範囲は次のように表せる。

$\int_{C_1} \frac{e^{iz}}{z} dz=\int_ε^R \frac{e^{ix}}{x} dx$

右辺の変数が $x$ に戻っているが、これは積分範囲が実軸上、つまり実数に限られているから、実数の変数としてよく使われる $x$ に戻しただけである。この積分は一旦放置する。

$C_2$ における積分

$C_1$ と同様にして、 $C_2$ での積分範囲を次のように表す。この経路は半径 $R$ の半円の形をしていることから、極座標を使った方が簡単に考えられそうだ。 $z=Re^{iθ}$ とおいて積分する。積分範囲は、積分変数が角度 $θ$ になることに注意すると、 $0$ から $π$ となる(これがわからなかったら複素数の極座標表示を復習すること)。

$\begin{eqnarray} \int_{C_2} \frac{e^{iz}}{z} dz&=&\int_0^π \frac{e^{iRe^{iθ}}}{Re^{iθ}} \frac{dz}{dθ}dθ\\&=&\int_0^π \frac{e^{iR(cosθ+isinθ)}}{Re^{iθ}} R･ie^{iθ}dθ\\&=&\int_0^π ie^{iR(cosθ+isinθ)} dθ \end{eqnarray}$

この積分の絶対値をとる。

$\begin{eqnarray} \left| \int_{C_2} \frac{e^{iz}}{z} dz \right| &=& \left| \int_0^π ie^{iR(cosθ+isinθ)} dθ \right|\\&≤& \int_0^π \left| ie^{iR(cosθ+isinθ)}\right| dθ\\ &=&\int_0^π |i|･|e^{iRcosθ}|･|e^{i^2Rsinθ}|dθ\\ &=&\int_0^π 1･1･e^{-Rsinθ}dθ\\&=& \int_0^π e^{-Rsinθ}dθ\\&=& \int_0^{π/2} e^{-Rsinθ}dθ+\int_{π/2}^π e^{-Rsinθ}dθ\\&=&2\int_0^{π/2} e^{-Rsinθ}dθ \end{eqnarray}$

途中の不等式の意味が分からなかったら三角不等式を思い出してみよう。

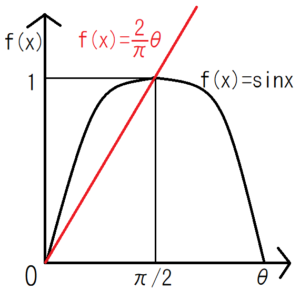
この図から、 $0<θ<\frac{π}{2}$ の範囲では、 $\frac{2}{π}<sinx$ だとわかる。これを使ってさらに積分を変形する。

$\begin{eqnarray} \left| \int_{C_2} \frac{e^{iz}}{z} dz \right| &=&2\int_0^{π/2} e^{-Rsinθ}dθ\\&≤&2\int_0^{π/2} e^{-R･\frac{2}{π}θ}dθ\\&=&2･\left[ -\frac{π}{2R}e^{-R･\frac{2}{π}θ} \right]_0^{π/2}\\&=&\frac{π}{R} \left( 1-e^{-R} \right)\\&→&0 \quad (R→∞) \end{eqnarray}$

よって、 $R→∞$ としたとき、経路 $C_2$ の積分は $0$ になる。

$\int_{C_2} \frac{e^{iz}}{z} dz→0 \quad (R→∞)$

ちなみにこれの被積分関数を $f(x)$ と一般化したものをジョルダンの補題という。

$C_3$ における積分

$C_3$ での積分を考える。ほとんど $C_1$ のときと同じであるが、符号に気を付ける。

$\begin{eqnarray}\int_{C_3} \frac{e^{iz}}{z} dz&=&\int_{-R}^{-ε} \frac{e^{ix}}{x} dx\\&=&\int_{R}^{ε} \frac{e^{-it}}{-t} (-dt)\\&=&\int_{R}^{ε} \frac{e^{-it}}{t} dt\\&=&-\int_{ε}^{R} \frac{e^{-it}}{t} dt \end{eqnarray}$

途中で $x=-t$ とおいた。変数は何を使ってもいいから、 $t$ を $x$ に変えれば、この計算を次のようにまとめられる。

$\int_{C_3} \frac{e^{iz}}{z} dz=-\int_{ε}^{R} \frac{e^{-ix}}{x} dx$

$C_1$ と同様に、これも一旦放置する。

$C_4$ における積分

$C_4$ での積分範囲を考える。 $e^{iz}$ をマクローリン展開すれば、 $\frac{e^{iz}}{z}$ は次の形をしていることがわかる。

$\begin{eqnarray} \frac{e^{iz}}{z}&=&\frac{1}{z} \left( 1+iz+\frac{(iz)^2}{2!}+… \right) \\&=&\frac{1}{z}+\frac{1}{z}\left( iz+\frac{(iz)^2}{2!}+… \right) \\&=&\frac{1}{z}+g(z) \end{eqnarray}$

後は $C_2$ のときと似ているが、半径が $ε$ になっていることに気を付ける。さらに積分する方向に注意すると、積分範囲が $π$ から $0$ になっていることがわかる。

$\begin{eqnarray} \int_{C_4} \frac{1}{z} dz&=&\int_π^0 \frac{1}{εe^{iθ}} \frac{dz}{dθ}dθ \\&=&\int_π^0 \frac{1}{εe^{iθ}} ε･ie^{iθ}dθ\\&=&-i\int_0^π dθ\\&=&-i\left[ θ\right]_0^π\\&=&-iπ\end{eqnarray}$

次に $g(z)$ の積分を考える。 $g(z)$ は $\frac{1}{z}$ と違い、 $z=0$ で正則である。よって、 $z$ が $0$ に近いならば、 $|g(z)|≤M$ を満たす正の数 $M$ が存在する。だから、次のように変形できる。

$\begin{eqnarray} \left| \int_{C_4} g(z) dz\right|&≤&\int_0^π \left| g(z) iεe^{iθ} \right| dθ\\&≤&\int_0^π Mε dθ\\&=&πMε→0 \quad (ε→+0) \end{eqnarray}$

以上より、 $C_4$ での積分は、次のようにまとめられる。

$\begin{eqnarray} \int_{C_4} \frac{e^{iz}}{z} dz&=&\int_{C_4} \frac{1}{z}dz+\int_{C_4} g(z) dz\\&=&-iπ \quad (ε→+0) \end{eqnarray}$

各積分範囲での積分結果の代入

これまでの積分結果を、コーシーの積分定理の式に代入する。

$\begin{eqnarray} 0&=&\int_{C_1} \frac{e^{iz}}{z} dz+\int_{C_2} \frac{e^{iz}}{z} dz+\int_{C_3} \frac{e^{iz}}{z} dz+\int_{C_4} \frac{e^{iz}}{z} dz\\&=&\int_ε^R \frac{e^{ix}}{x} dx+0-\int_{ε}^{R} \frac{e^{-ix}}{x} dt-iπ\\&=&\int_ε^R \frac{e^{ix}-e^{-ix}}{x} dx-iπ\\&=&2i\int_ε^R \frac{e^{ix}-e^{-ix}}{2ix} dx-iπ\\&=&2i\int_ε^R \frac{sinx}{x} dx-iπ\end{eqnarray}$

$ε→0$ , $R→∞$ という極限をとって、最終的な答えがでる。

$\int_0^∞ \frac{sinx}{x} dx=\frac{π}{2}$

参考文献

・谷口健二・時弘哲治(2016)『理工系の数理複素解析』,裳華房.

・渡部隆一・宮崎浩・遠藤静男(1980)『改訂工科の数学4 複素関数』,培風館.

複素積分における積分経路の設定方法

特異点を避けて積分範囲を設定する