複素積分の解き方は、コーシーの積分定理や留数定理を利用するものや、自分で特定の積分経路を指定するものなど、様々な種類がある。問題を解くときはそれらを適切に使い分けなければいけないが、すべての方法が頭に入っていなければ土俵に上がることすらもできない。この記事では、定理を使う複素積分の解き方のパターンをまとめてみようと思う。
この記事では以前紹介した「正則」という単語が重要になるため、先にコーシー・リーマンの方程式の記事を読むことをお勧めする。
目次
コーシーの積分定理を使った複素積分
コーシーの積分定理とは
複素積分経路Cが単一閉曲線で、かつ関数\(f(z)\)が経路C上とその内部ですべて正則ならば、次の式が成り立つ。
$$\int_{C} f(z) dz=0$$
例題
問題:関数\(f(z)=z^{3}\)を、\(|z|=1\)を積分経路として複素積分しなさい
この積分経路は、複素平面上で考える必要がある。複素平面とは、横軸に複素数の実部、縦軸に虚部をとった平面座標のことである。横軸を実軸、縦軸を虚軸という。
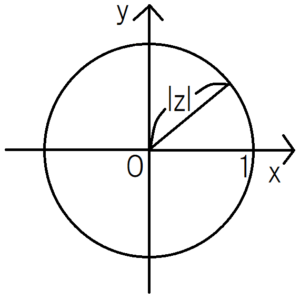
ここで、複素平面上における\(|z|=1\)とは、原点\(|z|=0\)を中心とする半径\(1\)の円のことを表す。直感的にわからない方のために、少し詳しく説明する。\(z=x+iy\)とすると、下の図と三平方の定理から、\(|z|=\sqrt{x^{2}+y^{2}}\)となる。\(|z|=1\)を代入した後にこの式の両辺を二乗すると、\(x^{2}+y^{2}=1\)が得られる。この式は、中学や高校で学習した円を表す式と一致する。
積分範囲の意味を確認したところで、本題に入る。前回の記事から、\(f(z)=z^{3}\)にコーシー・リーマンの方程式を適用すれば、この関数\(f(z)\)はあらゆる場所で正則であることがわかる。したがって、コーシーの積分定理によって、求めたい複素積分が求まる。
$$\int_{|z|=1} z^{3} dz=0$$
次に留数定理を紹介したいが、その前に前提知識としてローラン展開と留数を紹介したい。
ローラン展開の概要
ローラン展開とは、テイラー展開を負冪(マイナス乗)まで拡張したようなものである。
$$f(z)=\sum_{n=-∞}^{∞} {a_{n}(z-α)^{n}}$$
留数の概要
留数とは、関数\(f(z)\)をローラン展開したときの\((z-α)^{-1}\)の係数、つまり\(a_{-1}\)のことを指す。
\(z=α\)における関数\(f(z)\)の留数を次のように表す。
$$a_{-1}=Res(α,f(z))$$
留数定理を使った複素積分
留数定理は、つぎのようになる。
ここで\(k\)は、関数\(f(z)\)が積分経路C上またはその内部にもつ、正則でない点の数を表す。
コーシーの積分定理では、積分経路とその内部が正則の場合を考えたが、もし正則でない点が含まれていたらどうなるだろうか。この場合、正則でない点における\(f(z)\)の留数を求めることで、複素積分を求めることができる。
関数\(f(z)\)の極\(z=α\)がn位の極の場合、留数\(Res(α,f)\)は次のように表せる。
例えば、関数\(f(z)\)の極\(z=α\)が1位の極の場合、留数\(Res(α,f)\)は次のように表せる。
例題
問題1:関数\(f(z)=\frac{1}{z}\)を、\(|z|=1\)と\(|z-5i|=1\)をそれぞれ積分経路として複素積分しなさい。
・\(|z|=1\)について
\(f(z)=\frac{1}{z}\)は、\(z=0\)でのみ正則でない。そして\(z=0\)は積分経路\(|z|=1\)の内部にある点である。さらに、\(f(z)=\frac{1}{z}\)の留数は明らかに\(1\)である。
後は留数定理に代入すれば、求めたい複素積分が求まる。
積分経路を指定して複素積分する方法
参考文献
・占部博信(1999)『数学基礎コース=K4 基礎課程 複素関数論』,サイエンス社.
・谷口健二・時弘哲治(2016)『理工系の数理 複素解析』,裳華房.

