[mathjax]
マクスウェル方程式から、誘電率や透磁率が異なる物質の境界における電場・磁場の様子が求められる。この記事では、マクスウェル方程式の積分形を用いて、電場と磁場の境界条件について考える。
電束密度と電場について
電束密度の境界
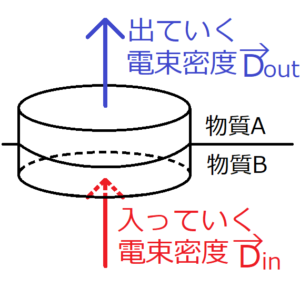
ガウスの法則の積分形を考える。ただし、\(ρ=0\)を仮定する。
ここで、異なる誘電率をもつ物質の境界をまたがるような底面積\(S\)の微小円筒を考える。さらに、その微小円筒の底面から、電束密度\(\bf D\)が出入りしている。ここで、閉曲面\(S\)に入ってくる電束密度を\({\bf D}_{in}\)、出ていく電束密度を\({\bf D}_{out}\)とする。それらの合計は0であるから、入ってくる電束密度を正とすると、次の関係がいえる。
\({\bf D}_{out}\)を移項させる。
この式は、異なる誘電率をもつ物質の境界において、電束密度の法線成分(境界面に対して垂直な成分)が等しくなることを意味する。つまり、境界を越えたからといって、境界面に対して垂直に入ってきた電束密度が、不連続的に小さくなったり大きくなったりすることはない。
電場の境界
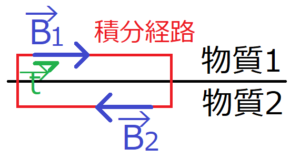
電場の境界を考えるときは、異なる物質の境界をまたがるような長方形の線積分を考える。
今、その長方形の長辺を境界面と平行、短辺を垂直となるようにする。さらに、長辺の長さは\(l\)、短辺の長さは無限小とする。
この積分経路を意識して、ファラデーの法則
の左辺を線積分する。ただし、時間変化する外部磁場が存在しない(\(\frac{∂{\bf B}}{∂t}=0\))とする。
ここで\(\bf t\)を、\({\bf E}_1\)に平行かつ単位長さのベクトルとした。
ファラデーの法則より上の式が0になるから、\(\bf t\)と\(l\)の大きさが0になりえないことに注意すると、次の関係が求まる。
この式は、異なる誘電率をもつ物質の境界において、電場の接線成分(境界面に平行な成分)が等しくなることを意味する。
磁束密度と磁場について
磁束密度の境界
磁化保存則の式の積分形
を、電束密度の境界を考えたときと同じ微小円筒を積分範囲と設定することで、磁束密度の境界条件も求まる。
この微小円筒に入ってくる磁束密度\({\bf B}_{in}\)と磁束密度\({\bf B}_{out}\)の合計は0であるから、入ってくる磁束密度を正とすると、次の関係がいえる。
\({\bf B}_{out}\)を移項させる。
この式は、異なる誘電率をもつ物質の境界において、磁束密度の法線成分が等しくなることを意味する。
磁場の境界
アンペールの法則の積分形
を、電場の境界を考えたときと同じ長方形の外周を積分範囲と設定することで、磁束密度の境界条件も求まる。ただし、電流と時間変化する外部電場が存在しない(\({\bf i}=0,\frac{∂{\bf D}}{∂t}=0\))とする。
アンペールの法則よりこれが0になるということだから、次の関係が求まる。
この式は、異なる誘電率をもつ物質の境界において、磁場の接線成分が等しくなることを意味する。
まとめ
・マクスウェル方程式の積分形を使って、電場と磁場の境界条件について考えた。
・電束密度と磁束密度は法線方向、電場と磁場は接線方向の大きさが、境界面において連続となる。
参考文献
・伊東敏雄(2008)『朝倉物理学選書2 電磁気学』,朝倉書店.
・砂川重信(1988)『電磁気学 ―初めて学ぶ人のために―』,培風館.

