[mathjax]
デルタ関数\(δ(x-a)\)とは、カッコの中が\(0\)のときのみ特殊な値になるようなものであり、次のようにして定義される。
$$\int_{-∞}^∞ f(x)δ(x-a)dx=f(a)$$
このデルタ関数は名前に関数とついているが、正確には関数ではない。そのため、このように積分を使って定義される。
電磁気学
ローレンツゲージとは
ゲージ変換を導入すれば、電磁ポテンシャルが満たす式を次のようにきれいな形に変形できる。
$$\left( ∇^2-\frac{1}{c^2}\frac{∂^2}{∂t^2} \right){\bf A}(t,{\bf r})=-μ_0{\bf j}(t,{\bf r})$$
$$\left( ∇^2-\frac{1}{c^2}\frac{∂^2}{∂t^2} \right)φ=-\frac{1}{ε_0}ρ$$
ポインティングベクトルの意味と絶対値
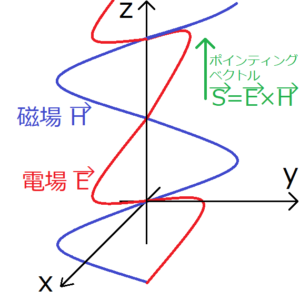
ポインティングベクトル\({\bf S}(t,{\bf r})\)とは、電磁場の流れを表すものであり、次のように定義される。
$${\bf S}({\bf r},t)={\bf E}({\bf r},t)×{\bf H}({\bf r},t)$$
ジュールの法則とその微分形の導出
ジュールの法則
$$W=IΔφ=RI^2=\frac{(Δφ)^2}{R}$$
\(W\):単位時間あたりで2点間で発生する熱量 \(Δφ\):2点間の電位差 \(R\):2点間の抵抗 \(I\):2点間を流れる電流
ジュールの法則の微分形
$$w({\bf r})={\bf j}({\bf r})･{\bf E}({\bf r})$$
\(w\):単位体積内かつ単位時間で発生する熱量 \({\bf j}\):電流密度 \({\bf E}\):電場
オームの法則とその微分形の導出
オームの法則
$$Δφ=RI$$
\(Δφ\):2点間の電位差 \(R\):2点間の抵抗 \(I\):2点間を流れる電流
オームの法則の微分形
$${\bf j}=σ{\bf E}$$
\({\bf j}\):電流密度 \(σ\):電気伝導率 \({\bf E}\):電場
電磁ポテンシャルとゲージ変換の導出
スカラーポテンシャル\(φ\)とベクトルポテンシャル\({\bf A}\)をまとめて電磁ポテンシャルと呼ぶ。
$${\bf E}(t,{\bf r})=-∇φ(t,{\bf r})-\frac{∂{\bf A}(t,{\bf r})}{∂t}$$
$${\bf B}(t,{\bf r})=∇×{\bf A}(t,{\bf r})$$
電場\({\bf E}(t,{\bf r})\)と磁束密度\({\bf B}(t,{\bf r})\)は、次のゲージ変換で不変である。
$${\bf A}→{\bf A}'(t,{\bf r})={\bf A}(t,{\bf r})+∇χ(t,{\bf r})$$
$$φ(t,{\bf r})→φ'(t,{\bf r})=φ(t,{\bf r})-\frac{∂}{∂t}χ(t,{\bf r})$$
Maxwell方程式の微分形と積分形
ガウスの法則
$$div {\bf D}({\bf r},t)=ρ({\bf r},t)$$
磁束保存則
$$div {\bf B}({\bf r},t)=0$$
アンペール・マクスウェルの法則
$$rot {\bf H}({\bf r},t)={\bf i}({\bf r},t)+\frac{∂{\bf D}({\bf r},t)}{∂t}$$
ファラデーの誘導法則
$$rot {\bf E}({\bf r},t)=-\frac{∂{\bf B}({\bf r},t)}{∂t}$$
電場と電束密度、磁場と磁束密度の関係式
$${\bf D}({\bf r},t)=ε{\bf E}({\bf r},t)$$
$${\bf B}({\bf r},t)=μ{\bf H}({\bf r},t)$$
\({\bf E}({\bf r},t)\):電場 \({\bf D}({\bf r},t)\):電束密度 \({\bf H}({\bf r},t)\):磁場 \({\bf B}({\bf r},t)\):磁束密度
\(ρ({\bf r},t)\):電荷密度 \({\bf i}({\bf r},t)\):電流密度 \(ε\):誘電率 \(μ\):透磁率
最初の4つの方程式をまとめてMaxwell方程式という。この形式を、Maxwell方程式の微分形という。後の2つは補足として電場と電束密度、磁場と磁束密度の関係式をそれぞれ書いた。