ガウスの法則とは、電場\(\bf E\)と電荷密度\(ρ\)の関係式のことである。この法則は、マクスウェル方程式の一つとされるほど、電磁気学において重要なものである。
この記事では、ガウスの法則の導出を行う。
電磁気学
電位とは
[mathjax]
電荷には、電場を発生させる能力がある。そして、重力ポテンシャルと同様にして、電場によるポテンシャルも考えることができる。このポテンシャルのことを電位と呼ぶ。
この記事では、電位をポテンシャルエネルギーの式から求めてみる。
電場をクーロン力の式から定義する
[mathjax]
前の記事では電荷とは何かを考えたが、この電荷は、周囲の空間に影響を及ぼすことができる。このような周囲の空間への影響のことを一般的に場とよぶのだが、特に電荷がつくる場のことを電場という。
この記事では、一つの電荷が作り出す電場について考える。
参考:電荷とクーロンの法則
誘電体と分極
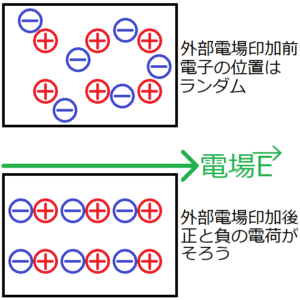
誘電体とは、外部電場をかけたときに分極するような物体のことである。誘電体は電気を通さないため、不導体とも呼ばれる。コンデンサーの間に挿入すると、電気容量が大きくなる。
この記事では、電束密度と分極ベクトルの定義を確認した後、公式\({\bf D}=ε{\bf E}\)を導出する。
電荷とクーロンの法則
[mathjax]
髪の毛に下敷きをこすって逆立てる遊びを小さいころにした人は多いだろう。この現象が起こる理由は、片方の物体に含まれている電荷がもう片方に移動することで、それぞれの物体が違う種類の電荷によって帯電するからである。
磁化率と残留磁化
[mathjax]
外部磁場が0のときに磁化ベクトルも0になる等方的な物質において、外部磁場が小さいとき、磁化ベクトル\(\bf M\)は外部磁場\({\bf H}_{ex}\)に比例する。この比例定数を磁化率\(χ_m\)という。
$${\bf M}=χ_m{\bf H}_{ex}･･･(1)$$
この磁化率が正の場合は常磁性体か強磁性体、負の場合は反磁性体を表す。
磁化を考慮したマクスウェル方程式の導出
[mathjax]
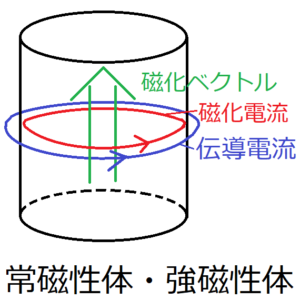
鉄芯が挿入されているコイルに電流を流すと、その鉄芯の表面に磁化電流が流れるようになる。この磁化電流による電流によって発生する磁場を、磁化ベクトルという。磁化ベクトルは、本によって\({\bf M}\)や\({\bf J}\)と表記される。厳密には、古典的には磁化ベクトルは発生しないが、量子力学導入までは暫定的にこのように磁化ベクトルを定義しておく。
ビオ・サバールの法則
ビオ・サバールの法則
ビオ・サバールの法則とは、位置\({\bf r}\)における、電流による磁束密度\({\bf B}\)を表す式である。この式はビオとサバールによって行われた実験によって求められたものである。
$$d{\bf B}=\frac{μ_0}{4π}･\frac{Id{\bf s}×{\bf r}}{r^3}$$
\(d{\bf s}\):電流が進む向きを表すベクトル \(I\):電流の強さ
位置\({\bf r}\)における磁束密度\({\bf B}\)を求めるには、上の式の両辺を積分すればよい。この式の右辺に含まれている微小量は\(d{\bf s}\)であるため、電流の通り道に沿って積分する。
古典的・量子力学的に考える磁化
[mathjax]
量子力学が提唱されるはるか昔に、アンペールは、古典的な視点から磁化を説明した。それによると、磁化は分子電流によって発生するものとされている。ところが量子力学誕生後、磁化は電子のスピン(自転)などによるものであることが分かってきた。この記事では、磁化を古典的・量子的の両方の視点から見てみる。
静電場と静磁場中の電荷の運動方程式
[mathjax]
静磁場(時間変化しない磁場)\({\bf B}({\bf r})\)中を、\(Δ{\bf r}\)方向に流れる電流\(I\)にかかる力を、アンペールの力という。この力を\({\bf F}_B({\bf r})\)とおくと、次の式を満たす。
$${\bf F}_B({\bf r})=IΔ{\bf r}×{\bf B}({\bf r})$$
この式を使って、静電場と静磁場中の電荷が満たす運動方程式を導出する。