大学ではLRC電気回路を考えることが多い。Lはコイル、Rは抵抗、Cはコンデンサーを指す。それぞれの部品にかかる電圧と、部品に流れる電流の関係は、次のように与えられる。
コイルの電圧
$$V_{L}(t)=L\frac{dI(t)}{dt}$$
抵抗の電圧
$$V_{R}(t)=RI(t)$$
コンデンサーの電圧
$$V_{C}(t)=\frac{1}{C} \int I(t) dt=\frac{Q(t)}{C}$$
\(L\):コイルの自己インダクタンス \(R\):抵抗の大きさ \(C\):コンデンサーの電気容量 \(Q(t)\):コンデンサーに蓄えられている電荷
目次
コイルの特徴
中学、高校で学習したように、コイルは内部の磁場が変化することを嫌う。だから、もし外から磁石が近づいてきたら、その磁石をはじき返す方向に電流が流れる。この電流を誘導電流といった。
これを踏まえて、コイルと抵抗の直列回路上のコイルのふるまいを考える。最初に電流が流れていない状態から、直流電圧を印加したとする。すると、コイルは内部の状態が変化することを嫌うため、印加された電圧とは逆方向の誘導電流を流そうとする。この誘導電流を流そうとしてコイルが発生させる電圧を、コイルの逆起電力という。ただし、この逆起電力にも限界はあるため、電圧を印加し続ければ、次第に印加した方向に電流が流れるようになる。そして、最終的には逆起電力は0になり、抵抗によって流れる電流は一定になる。
この状態で、回路のスイッチを切ったらどうなるか。コイルは内部の状態が変化することを嫌うため、電圧を印加していた方向に逆起電力が発生して、なんとかして元の状態を維持しようとする。ところが時間がたつにつれてその逆起電力も消えていき、最終的には0になる。
RL直列回路
このことを数式を使って考えてみる。コイルと抵抗の直列回路を図にすると、次のようになる。
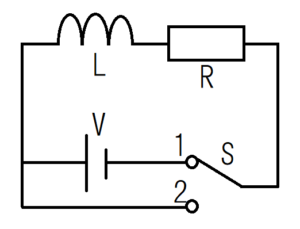
このような回路を、RL直列回路とよぶ。コイルと抵抗にかかる電圧の和\(V_{L}+V_{R}\)と、印加する電圧\(V\)の和は等しいため、次の式が成り立つ。
$$L\frac{dI(t)}{dt}+RI(t)=V$$
スイッチ1を入れたときの挙動
\(t=0\)のときにスイッチ\(S\)を1に入れる。スイッチ1に入れた瞬間(\(t=0\))は、コイルの逆起電力によって、回路に電流は流れない(\(I(0)=0\))。この初期条件をもとに上の微分方程式を解くと、次の式が得られる。
$$I(t)=\frac{V}{R}(1-e^{-\frac{R}{L}t})$$
時間が十分経過(\(t→∞\))したとき、\(e^{-\frac{R}{L}t}→0\)になるため、電流は\(I=\frac{V}{R}\)になる。この電流の値は、オームの法則より、直列回路に抵抗\(R\)のみが存在するときのものと一致する。このことからも、\(t→∞\)でコイルの逆起電力が0になることがわかる。上の\(I(t)\)をグラフ化すると、下のようになる。
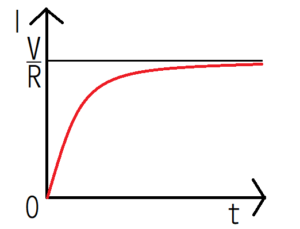
スイッチ2を入れたときの挙動
次に、スイッチ1に入れて十分時間が経過した後、電源が無いスイッチ2に切り替えたときの時刻を\(t=0\)としたときの電流\(I(t)\)の変化を調べる。上の方程式と違い、回路上に電源が存在しなくなるため、\(V=0\)となる。
$$L\frac{dI(t)}{dt}+RI(t)=0$$
これを初期条件(\(t=0⇒I(0)=\frac{V}{R}\))を使って解くと、
$$I(t)=\frac{V}{R}e^{-\frac{R}{L}t}$$
この式から、スイッチ2に切り替えた直後では電流は流れるが、時間が経過するにつれて弱くなっていくことがわかる。最後に、この\(I(t)\)をグラフ化する。
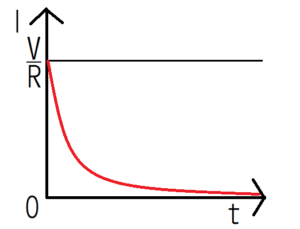
抵抗の特徴
オームの法則より、\(V_{R}=RI\)である。
ちなみに、電流密度\({\bf j}\)と電気伝導率\(σ\)、電場\({\bf E}\)の関係式\({\bf j}=σ{\bf E}\)もあるが、これもオームの法則という。
コンデンサーの特徴
コンデンサーは、電荷をためる性質をもつ。どのくらいの電荷をためられるかを表す指標として、静電容量\(C\)という指標がある。
導体板を向かい合わせるだけで、最も簡単な構造のコンデンサーが完成する。下の式より、この導体板の間に誘電体や絶縁体を挟むことで、静電容量\(C\)が大きくなることがわかる。
$$C=ε\frac{S}{d}=ε_{0}ε_{r}\frac{S}{d}$$
\(S\):導体板の面積 \(d\):導体板間の距離 \(ε\):誘電体・絶縁体の誘電率 \(ε_{0}\):真空中の誘電率 \(ε_{r}\):誘電体・絶縁体の比誘電率
電荷を持たないコンデンサーに電流を流すと、そのコンデンサーは電荷を蓄え始める。電荷がない状態では、コンデンサーの抵抗が0であると考えてよい。ところが、徐々に電荷がたまるにつれて、回路に電流が流れなくなってくる。最終的に、電荷が最大までたまって充電が終わると、回路に電流が流れなくなる。
RC直列回路
このことを数式を使って考えてみる。次のように、コンデンサーと抵抗のが直列に接続されている回路を考える。
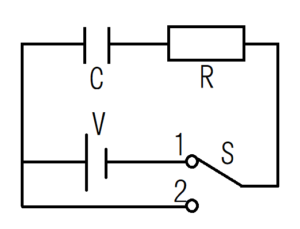
このような回路を、RC直列回路とよぶ。コンデンサーと抵抗にかかる電圧の和\(V_{C}+V_{R}\)と、印加する電圧\(V\)の和は等しいため、次の式が成り立つ。
$$\frac{1}{C} \int I(t) dt+RI(t)=V$$
スイッチ1を入れたときの挙動
コンデンサーに含まれる電荷を\(q(t)\)とすると、電流\(I(t)\)と電荷\(Q(t)\)の関係式\(\frac{1}{C} \int I(t) dt=q(t)\)より、方程式を書き換える。
$$q(t)+RC\frac{dq(t)}{dt}=VC$$
\(t=0\)でコンデンサーに電荷が無いとすると、初期条件は\(q(0)=0\)となる。これに沿って微分方程式を解くと、次のようになる。
$$q(t)=VC(1-e^{-\frac{1}{RC}t})$$
上の電流\(I(t)\)と電荷\(Q(t)\)の関係式から、両辺を\(t\)で微分すると、\(I(t)\)に関係する式が求まる。
$$I(t)=\frac{V}{R}e^{-\frac{1}{RC}t}$$
この式から、\(t=0\)のときの電流は\(I(t)=\frac{V}{R}\)となり、コンデンサー自身の抵抗は0である。ところが\(t→∞\)のときは\(I(t)→0\)だから、十分時間が経過して充電が終わったら、回路に電流が流れなくなることが確認できた。
グラフの形はRL回路のスイッチ2を入れたときの挙動と同じであるため、省略する。
スイッチ2を入れたときの挙動
次に、十分コンデンサーが充電された状態でスイッチ2に切り替えたときを考える。上の式から、\(t→∞\)のときのコンデンサーの電荷は、\(q(t)=VC\)となる。
\(I(t)\)に関する最初の方程式の両辺をtで微分すると、次のようになる。
$$\frac{1}{C} I(t)+R\frac{dI(t)}{dt}=0$$
初期条件\(I(0)=-\frac{V}{R}\)から、この微分方程式を解いて、次の式を得る。初期条件の符号が負になっている理由は後述する。
$$I(t)=-\frac{V}{R}e^{-\frac{1}{RC}t}$$
スイッチ1を入れたときと似た関数になった。この式から、スイッチ2に切り替えると、コンデンサーに充電されていた電荷が放出されて、それがすべて出きったら電流が0になることがわかる。
ただし、スイッチ1を入れたときとは正負が逆転していることに注意する。符号が逆になる理由は、スイッチを変えると電子や正孔(ホール)の流れる方向が逆になるからである。
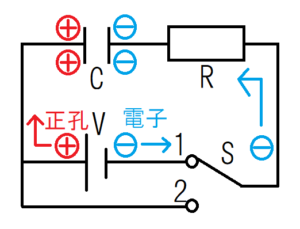
スイッチ1につないでいるときは、電子は回路を左回りに動き、コンデンサーの右側の板にたまる。一方、正孔は回路を右回りに動き、コンデンサーの左側の板にたまる。
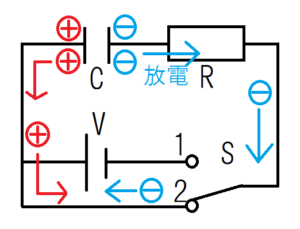
その後スイッチ2に接続すると、電子はコンデンサーの右側の板から放出され、回路を右回りに動く。一方、正孔はコンデンサーの左側の板から放出され、回路を左回りに動く。スイッチ1の図と比較すると、電子と正孔の向きが逆向きになっているから、電流の向きも逆になっている。よって、初期条件にはマイナスをつけなければならない。
まとめ
・コイルは、逆起電力によって、コイルに印加された電圧とは逆方向の電圧を発生させる。
・コンデンサーは、充電中は回路に電流を流すが、充電が終わったら電流を流さなくなる。
参考文献
・TDK(n.d)「コンデンサ編 No.1 『コンデンサの基礎知識』 | エレクトロニクス入門 | TDKマガジン | TDK株式会社」,(http://www.tdk.co.jp/techmag/electronics_primer/vol1.htm).
・長谷川修司(2009)『講談社基礎物理学シリーズ 2 振動・波動』,講談社.

