[mathjax]
ここでいう分布関数とは、とあるエネルギー準位に入る粒子の量を表すもので、エネルギーと粒子数のグラフで表現される。そして、粒子にはボーズ粒子とフェルミ粒子の2種類存在するが、それぞれの分布関数は異なる。
ボーズ粒子の分布関数のことをボーズ分布関数またはボーズ-アインシュタイン分布、またフェルミ粒子の分布関数のことをフェルミ分布関数またはフェルミ-ディラック分布とよぶ。
この記事では、大分配関数を使って、それぞれの分布関数を導出する。
参考:大分配関数とグランドカノニカル分布の導出
参考:フェルミ粒子とボーズ粒子の波動関数の導出
今回の系の確認
体積\(V\)の立方体の箱に、\(N\)個の粒子が入っている。この粒子は箱を出入りせず、\(N\)は一定とする。さらに、粒子がとることができるエネルギー準位の総数を\(n\)とする。
この\(N\)個の粒子のうち、エネルギー準位\(ε_j\)をとるものが\(N_j\)個存在するものとする。こうすると、エネルギー準位\(ε_j\)をとる粒子の総エネルギーは\(ε_jN_j\)となる。
したがって、系の総粒子数\(N\)は
$$\displaystyle N=\sum_{j=1}^nN_j$$
となる。一方系の総エネルギー\(E\)は、あらゆる準位の粒子の総エネルギーの合計になるため、次のようになる。
$$\displaystyle E=\sum_{j=1}^nε_jN_j$$
大分配関数の導出
大分配関数は次のように定義される。
$$\displaystyle Ξ≡\sum_σ e^{-\frac{1}{k_BT}・E_σ+\frac{μ}{k_BT}・N_σ}$$
参考:大分配関数とグランドカノニカル分布の導出
上の定義式の系の総エネルギー\(E_σ\)と総粒子数\(N_σ\)に、今回の系のそれぞれの値を代入すればよい。
これ以降、ボーズ粒子とフェルミ粒子のそれぞれの大分配関数を求める。
ボーズ粒子の場合
ボーズ粒子にはパウリの排他律は適応されないため、複数の粒子が同じ量子状態をとることができる。この例として、BCS理論での超電導が挙げられる。電子がクーパー対をつくると、その対全体を1つのボーズ粒子とみなせる。そして、超電導物質が特定の環境下におかれたときに、すべてのボーズ粒子が最低のエネルギー準位に落ち込むことで、超電導が現れる。
ボーズ粒子は同じエネルギー準位にいくつでも入れるため、0粒子系から無限大個の粒子系まで考えることができる。したがって、下の粒子数に関する和\(\sum_{N_j}\)の範囲は、\(0\)から\(∞\)となる。
\begin{eqnarray}\displaystyle Ξ&≡&\sum_σ e^{-\frac{1}{k_BT}・E_σ+\frac{μ}{k_BT}・N_σ}\\&=&\sum_{N_1=0}^∞\sum_{N_2=0}^∞・・・\sum_{N_n=0}^∞ \left(e^{-\frac{1}{k_BT}[(ε_1N_1+ε_2N_2+・・・+ε_nN_n)-μ(N_1+N_2+・・・+N_n)]}\right)\\&=&\sum_{N_1=0}^∞\sum_{N_2=0}^∞・・・\sum_{N_n=0}^∞ \left[\left(e^{-\frac{1}{k_BT}(ε_1-μ)}\right)^{N_1}\left(e^{-\frac{1}{k_BT}(ε_2-μ)}\right)^{N_2}・・・\left(e^{-\frac{1}{k_BT}(ε_n-μ)}\right)^{N_n}\right]\\&=&Ξ_1Ξ_2・・・Ξ_n\\&=&\prod_{j=1}^∞Ξ_j\end{eqnarray}
ここで、\(j\)番目のエネルギー準位に関する分配関数を\(Ξ_j\)とおいた。
$$Ξ_j=\sum_{N_j=0}^∞\left(e^{-\frac{1}{k_BT}(ε_j-μ)}\right)^{N_j}$$
この\(Ξ_j\)を、無限級数の公式
$$\displaystyle \sum^∞_{k=0} ar^k=\frac{a}{1-r} \ (|r|<1)$$
を使って変形させる。
$$Ξ_j=\frac{1}{1-e^{-\frac{1}{k_BT}(ε_j-μ)}} \ (ε_j>μ)$$
フェルミ粒子の場合
フェルミ粒子にはパウリの排他律が適応されるため、同じエネルギー準位に複数の粒子は入れない。つまり、1つのエネルギー準位に入る粒子の数は、0か1のどちらかとなる。
$$N_j=0 \ or \ 1$$
1つのエネルギー準位に1つまでしか粒子が入れないため、今回は\(n\)個までの粒子の分布を考えることができる。
この前提で、大分配関数を変形させる。
\begin{eqnarray}\displaystyle Ξ&=&\sum_{N_1=0,1}\sum_{N_2=0,1}・・・\sum_{N_n=0,1} \left[ \left(e^{-\frac{1}{k_BT}[(ε_1N_1+ε_2N_2+・・・+ε_nN_n)-μ(N_1+N_2+・・・+N_n)]}\right)\right]\\&=&\sum_{N_1=0,1}\sum_{N_2=0,1}・・・\sum_{N_n=0,1} \left[ \left(e^{-\frac{1}{k_BT}(ε_1-μ)N_1}\right)\left(e^{-\frac{1}{k_BT}(ε_2-μ)N_2}\right)・・・\left(e^{-\frac{1}{k_BT}(ε_n-μ)N_n}\right)\right]\\&=& \sum_{N_1=0,1}\left(e^{-\frac{1}{k_BT}(ε_1-μ)N_j}\right)\sum_{N_2=0,1}\left(e^{-\frac{1}{k_BT}(ε_2-μ)N_j}\right)・・・\sum_{N_n=0,1}\left(e^{-\frac{1}{k_BT}(ε_n-μ)N_j}\right)\\&=&\left(e^{-\frac{1}{k_BT}(ε_1-μ)・0}+e^{-\frac{1}{k_BT}(ε_1-μ)・1}\right)\left(e^{-\frac{1}{k_BT}(ε_2-μ)・0}+e^{-\frac{1}{k_BT}(ε_2-μ)・1}\right)・・・\left(e^{-\frac{1}{k_BT}(ε_n-μ)・0}+e^{-\frac{1}{k_BT}(ε_n-μ)・1}\right)\\&=&\left(1+e^{-\frac{1}{k_BT}(ε_1-μ)}\right)\left(1+e^{-\frac{1}{k_BT}(ε_2-μ)}\right)・・・\left(1+e^{-\frac{1}{k_BT}(ε_n-μ)}\right)\\&=&Ξ_1Ξ_2・・・Ξ_n\\&=&\prod_{j=1}^∞Ξ_j\end{eqnarray}
ここで、\(j\)番目のエネルギー準位に関する分配関数を\(Ξ_j\)とおいた。
$$Ξ_j=1+e^{-\frac{1}{k_BT}(ε_j-μ)}$$
以上で、ボーズ粒子とフェルミ粒子のそれぞれの場合における大分配関数を求められた。
分布関数の導出
大分配関数と粒子数
今回の最終目標は、大分配関数から、エネルギー準位と粒子数の関係を示す分布関数を求めることであった。そのためには、粒子数\(N\)を、大分配関数\(Ξ\)で表すことが不可欠である。
大分配関数を逆温度
$$β≡\frac{1}{k_BT}$$
を使って表すと、次のようになる。
$$\displaystyle Ξ≡\sum_σ e^{-β\left[E_σ-μN_σ\right]}$$
参考:大分配関数とグランドカノニカル分布の導出
この\(Ξ\)の式を眺めると、粒子数\(N_σ\)はネイピア数\(e\)の乗数に含まれていて、かつ\(μ\)の係数となっていることがわかる。したがって、\(N_σ\)を取り出すには、\(Ξ\)の自然対数\(lnΞ\)を\(μ\)で偏微分すればよさそうだ。
\begin{eqnarray}\frac{∂}{∂μ}lnΞ&=&-β\frac{∂}{∂μ}\sum_σ \left[E_σ-μN_σ\right]\\&=&β\sum_σ N_σ\end{eqnarray}
よって、\(j\)番目のエネルギー準位に入る粒子数の平均\(<N_j>\)は、次のようになる。
$$<N_j>=\frac{1}{β}\frac{∂}{∂μ}(lnΞ_j)$$
この\(<N_j>\)の式を、そのままエネルギー準位\(ε_j\)に依存する分布関数\(f_{β,μ}(ε_j)\)として定義する。
$$f_{β,μ}(ε_j)≡\frac{1}{β}\frac{∂}{∂μ}(lnΞ_j)$$
つまり、粒子数の平均\(<N_j>\)を計算することと分布関数\(f_{β,μ}(ε_j)\)を計算することは、完全に同じことである。
ちなみに、系全体の粒子の平均\(<N>\)を分布関数を使って表すには、それぞれのエネルギー準位における分布関数\(f_{β,μ}(ε_j)\)をすべて足せばよい。
$$\displaystyle <N>=\sum_{j=1}^∞f_{β,μ}(ε_j)$$
ボーズ粒子の場合
ボーズ粒子の大分配関数を、そのまま分布関数の定義式に代入すればよい。
\begin{eqnarray}f_{β,μ}(ε_j)&≡&\frac{1}{β}\frac{∂}{∂μ}(lnΞ_j)\\&=&\frac{1}{β}\frac{∂}{∂μ}\left[ln\left(\frac{1}{1-e^{-β(ε_j-μ)}}\right)\right]\\&=&\frac{1}{β}\frac{∂}{∂μ}\left[ln\left(1-e^{-β(ε_j-μ)}\right)^{-1}\right]\\&=&-\frac{1}{β}\frac{∂}{∂μ}\left[ln\left(1-e^{-β(ε_j-μ)}\right)\right]\\&=&-\frac{1}{β}\frac{1}{1-e^{-β(ε_j-μ)}}・\frac{∂}{∂μ}[1-e^{-β(ε_j-μ)}]\\&=&-\frac{1}{β}\frac{1}{1-e^{-β(ε_j-μ)}}・-βe^{-β(ε_j-μ)}\\&=&\frac{e^{-β(ε_j-μ)}}{1-e^{-β(ε_j-μ)}}\\&=&\frac{1}{e^{β(ε_j-μ)}-1}\end{eqnarray}
この分布関数をグラフ化する。
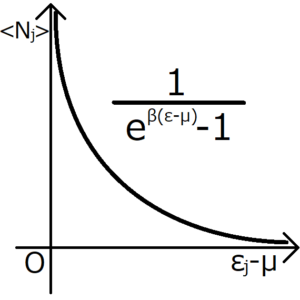
このグラフは、\(ε_j-μ\)が0に近づくにつれて、分布関数も無限大に発散していくことを示す。このことからも、一つのエネルギー準位に複数の粒子が入り得ることが確認できる。さらに、エネルギー準位が小さいほど、多くの粒子が入りやすくなることもわかる。
フェルミ粒子の場合
\begin{eqnarray}f_{β,μ}(ε_j)&≡&\frac{1}{β}\frac{∂}{∂μ}(lnΞ_j)\\&=&\frac{1}{β}\frac{∂}{∂μ}\left[ln\left(1+e^{-β(ε_j-μ)}\right)\right]\\&=&\frac{1}{β}\frac{1}{1+e^{-β(ε_j-μ)}}・\frac{∂}{∂μ}[1+e^{-β(ε_j-μ)}]\\&=&\frac{1}{β}\frac{1}{1+e^{-β(ε_j-μ)}}・βe^{-β(ε_j-μ)}\\&=&\frac{e^{-β(ε_j-μ)}}{1+e^{-β(ε_j-μ)}}\\&=&\frac{1}{e^{β(ε_j-μ)}+1}\end{eqnarray}
この分布関数をグラフ化する。
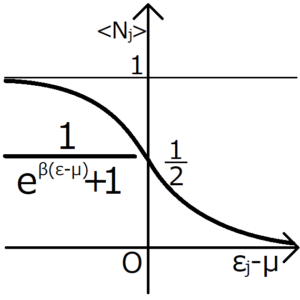
この分布関数はボーズ粒子のときと違い、決して1を超えない。このことからも、一つのエネルギー準位に複数の粒子が入らないことが確認できる。さらに、エネルギー準位が小さいほど、その準位に粒子が入っている確率が上がる。逆にエネルギーが大きいほど、その準位に粒子が入っている確率が下がる。
以上で、両方の粒子の場合の分布関数が求められた。
フェルミ分布の特徴
$$β=\frac{1}{k_BT}$$
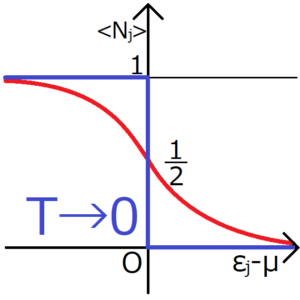
に注意すると、温度\(T\)の絶対零度の極限をとったとき\((T \to 0)\)、逆温度\(β\)は無限大に発散する\((β \to ∞)\)。このことをフェルミ分布
$$f_{β,μ}(ε_j)=\frac{1}{e^{β(ε_j-μ)}+1}$$
に適用してみる。
\(ε_j-μ>0\)の場合
分布関数中の\(e^{β(ε_j-μ)}\)の指数は\(+∞\)に発散する。これによって、分布関数の分母も無限大になるため、\(f_{β,μ}(ε_j)\)は0に近づく。
$$f_{β,μ}(ε_j) \to 0$$
\(ε_j-μ<0\)の場合
分布関数中の\(e^{β(ε_j-μ)}\)の指数は\(-∞\)に発散する。これによって、\(e^{β(ε_j-μ)}\)は0に近づくため、\(f_{β,μ}(ε_j)\)は1に近づく。
$$f_{β,μ}(ε_j) \to 1$$
以上を踏まえて分布関数をグラフにすると、下の図の青線のようなステップ関数上になる。
まとめ
ボーズ粒子の分配関数と分布関数
$$Ξ_j=\frac{1}{1-e^{-\frac{1}{k_BT}(ε_j-μ)}}$$
$$f_{β,μ}(ε_j)=\frac{1}{e^{β(ε_j-μ)}-1}$$
フェルミ粒子の分配関数と分布関数
$$Ξ_j=1+e^{-\frac{1}{k_BT}(ε_j-μ)}$$
$$f_{β,μ}(ε_j)=\frac{1}{e^{β(ε_j-μ)}+1}$$
フェルミ分布関数は、絶対零度の極限において、ステップ関数状になる。
参考文献
・小田垣孝(2003)『統計力学』,裳華房.
・藤井勝彦(1990)『統計力学』,マグロウヒル出版株式会社.
・村上雅人(2017)『なるほど統計力学』,海鳴社.