[mathjax]
シュレディンガー方程式を使えば、なぜボーズ粒子とフェルミ粒子の2種類の粒子が存在するのかがわかる。
この記事では、2粒子系のシュレディンガー方程式からわかる波動関数の対称性・反対称性から、ボーズ粒子とフェルミ粒子の波動関数を導出する。
ボーズ粒子・フェルミ粒子とは
ボーズ粒子とは、入れ替えに対して対称な粒子のことである。具体的には光子が挙げられる。
一方フェルミ粒子とは、入れ替えに対して反対称な粒子のことを指す。具体的には電子が挙げられる。
ボーズ粒子とフェルミ粒子の波動関数の導出
今回の2粒子系の確認
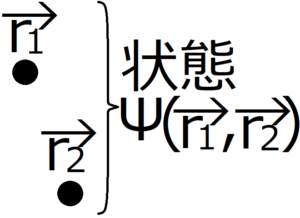
上の図のような同種の2つの粒子のみで構成された系を考える。この2粒子の状態を、まとめて波動関数\(Ψ({\bf r}_1,{\bf r}_2)\)で表す。
これ以降、\(Ψ({\bf r}_1,{\bf r}_2)\)を簡単に\(Ψ(1,2)\)と表すことにする。
参考:シュレディンガー方程式を解く意味とは
今回は簡単のため、粒子間の相互作用を無視する。
系のハミルトニアンの導出
今回の2粒子系全体の固有エネルギー\(E\)を導入すると、この系のシュレディンガー方程式は次のように書ける。
$$\left[-\frac{ħ^2}{2m}∇_1^2(1)-\frac{ħ^2}{2m}∇_2^2(2)+V_0(1,2)\right]Ψ(1,2)=EΨ(1,2)$$
ただし、粒子間の相互作用を無視するため、2粒子系全体のポテンシャルエネルギーは、それぞれの粒子のポテンシャルエネルギーの和となる。
$$V_0(1,2)=V_1(1)+V_2(2)$$
粒子1のハミルトニアンは
$${\hat H}_1=-\frac{ħ^2}{2m}∇_1^2(1)+V_1(1)$$
粒子2のハミルトニアンは
$${\hat H}_2=-\frac{ħ^2}{2m}∇_2^2(2)+V_2(2)$$
であるため、以上を考慮すると、最初のシュレディンガー方程式は次のように変形できる。
$$({\hat H}_1+{\hat H}_2)Ψ(1,2)=EΨ(1,2)$$
この式から、この系全体のハミルトニアン\(\hat H\)は、それぞれの粒子のハミルトニアンの和となる。
$${\hat H}={\hat H}_1+{\hat H}_2$$
系の固有エネルギーの導出
前提
粒子1が\(α\)という状態、粒子2が\(β\)という状態であると仮定する。ここでいう状態とは、量子数やスピンの状態のことを指す(つまり、量子数やスピンといった情報を、見栄えのため\(α\)や\(β\)という文字で置き換えただけ)。
これを考慮すると、それぞれの粒子で、次のシュレディンガー方程式が成立する。
$${\hat H}_1φ_α(1)=E_1φ_α(1)$$
$${\hat H}_2φ_β(2)=E_2φ_β(2)$$
本題
\(\hat H\)を導入すると、系のシュレディンガー方程式は次のようになる。
$${\hat H}Ψ(1,2)=EΨ(1,2)$$
ここで、波動関数\(Ψ(1,2)\)を変数分離させる。粒子の状態が\(α\)である場合と\(β\)である場合の波動関数をそれぞれ\(φ_α,φ_β\)で表すと、その変数分離は次のように書ける。
$$Ψ(1,2)=φ_α(1)φ_β(2)$$
この変数分離とそれぞれの粒子のハミルトニアンを、シュレディンガー方程式に代入する。
$$({\hat H}_1+{\hat H}_2)φ_α(1)φ_β(2)=Eφ_α(1)φ_β(2)・・・(1)$$
左辺を変形させる。粒子1のハミルトニアン\({\hat H}_1\)は粒子2の関数\(φ_β(2)\)には作用せず、同様に\({\hat H}_2\)は\(φ_α(1)\)に作用しない。
\begin{eqnarray}(左辺)&=&({\hat H}_1φ_α(1))φ_β(2)+φ_α(1)({\hat H}_2φ_β(2))\\&=&E_1φ_α(1)φ_β(2)+E_2φ_α(1)φ_β(2)\\&=&(E_1+E_2)φ_α(1)φ_β(2)\end{eqnarray}
以上より、2粒子系の固有エネルギー\(E\)は、それぞれの粒子の固有エネルギーの和となる。
$$E=E_1+E_2$$
粒子の入れ替えと波動関数\(φ\)の対称性・反対称性
粒子1と粒子2を入れ替えると、2粒子系の固有エネルギー\(E\)はどうなるだろうか。ここでは粒子1が状態\(β\)をとり、かつ粒子2が状態\(α\)をとる場合を考える。
まず、それぞれの粒子で、次のシュレディンガー方程式が成り立つだろう。
$${\hat H}_1φ_β(1)=E_1φ_β(1)$$
$${\hat H}_2φ_α(2)=E_2φ_α(2)$$
また、ここでは1と2を入れ替えるため、波動関数は\(Ψ(2,1)\)となる。
$${\hat H}Ψ(2,1)=EΨ(2,1)$$
ただし、波動関数\(Ψ(2,1)\)について、
$$Ψ(2,1)=φ_α(2)φ_β(1)$$
である。次に、このシュレディンガー方程式を前と同じように変形させる。
$$({\hat H}_1+{\hat H}_2)φ_α(2)φ_β(1)=Eφ_α(2)φ_β(1)$$
そして、この式の左辺は次のように変形できる。
\begin{eqnarray}(左辺)&=&({\hat H}_1+{\hat H}_2)φ_α(2)φ_β(1)\\&=&φ_α(2)({\hat H}_1φ_β(1))+({\hat H}_2φ_α(2))φ_β(1)\\&=&(E_1+E_2)φ_α(2)φ_β(1)\end{eqnarray}
以上より、粒子を入れ替えても
$$E=E_1+E_2$$
が成り立つことが分かった。
このことは、\(Ψ(1,2)\)と\(Ψ(2,1)\)はどちらも、ハミルトン\(\hat H\)に対して同じ固有エネルギーをつくることを意味している。
$${\hat H}Ψ(1,2)=EΨ(1,2)$$
$${\hat H}Ψ(2,1)=EΨ(2,1)$$
つまり、\(Ψ(1,2)\)と\(Ψ(2,1)\)は同じ量子状態をつくると言い換え可能だ。したがって、\(Ψ(1,2)\)と\(Ψ(2,1)\)の関数形が同じになる。(そもそも粒子1と粒子2は同種の粒子のため、両者の区別がつかない。このことからも、\(Ψ(1,2)\)と\(Ψ(2,1)\)の関数形が同じだといえる。)
両者の関数形が同じであるため、定数\(C\)を導入すると、次の関係を得る。
$$Ψ(1,2)=CΨ(2,1)$$
もう一度入れ替えると、
$$Ψ(1,2)=C^2Ψ(1,2)$$
となる。
この式から、定数\(C\)は、\(-1,+1\)のどちらかとなる。
$$C= \pm 1$$
このことから\(Ψ(1,2)\)は、\(C=+1\)の場合は対称性、
$$Ψ(1,2)=Ψ(2,1)$$
\(C=-1\)の場合は反対称性
$$Ψ(1,2)=-Ψ(2,1)$$
をもつ。
さらに、\(Ψ(1,2)\)と\(Ψ(2,1)\)がシュレディンガー方程式の固有関数になれることから、それらの線形結合
\begin{eqnarray}&&C_1Ψ(1,2)+C_2Ψ(2,1)\\&=&C_1φ_α(1)φ_β(2)+C_2φ_α(2)φ_β(1)\end{eqnarray}
もまた、そのシュレディンガー方程式の固有関数になれる。
線形和の規格化条件
\begin{eqnarray}1&=&\displaystyle \int\int|Ψ({\bf r}_1,{\bf r}_2)|^2d{\bf r}_1d{\bf r}_2\\&=&\int\intΨ^*({\bf r}_1,{\bf r}_2)Ψ({\bf r}_1,{\bf r}_2)d{\bf r}_1d{\bf r}_2\\&=&\int\int(C_1φ_α(1)φ_β(2)+C_2φ_α(2)φ_β(1))^*(C_1φ_α(1)φ_β(2)+C_2φ_α(2)φ_β(1))d{\bf r}_1d{\bf r}_2\\&=&\int\int(C^*_1φ^*_α(1)φ^*_β(2)+C^*_2φ^*_α(2)φ^*_β(1))(C_1φ_α(1)φ_β(2)+C_2φ_α(2)φ_β(1))d{\bf r}_1d{\bf r}_2\\&=&\int\int(C^*_1C_1φ^*_α(1)φ_α(1)φ^*_β(2)φ_β(2)+C^*_1φ^*_α(1)φ^*_β(2)C_2φ_α(2)φ_β(1) \\&& \qquad +C^*_2φ^*_α(2)φ^*_β(1)C_1φ_α(1)φ_β(2)+C^*_2C_2φ^*_α(2)φ_α(2)φ^*_β(1)φ_β(1))d{\bf r}_1d{\bf r}_2\\&=&\int\int(|C_1|^2φ^*_α(1)φ_α(1)φ^*_β(2)φ_β(2)+C^*_1φ^*_α(1)φ^*_β(2)C_2φ_α(2)φ_β(1) \\&& \qquad +C^*_2φ^*_α(2)φ^*_β(1)C_1φ_α(1)φ_β(2)+|C_2|^2φ^*_α(2)φ_α(2)φ^*_β(1)φ_β(1))d{\bf r}_1d{\bf r}_2\end{eqnarray}
\begin{eqnarray}(第一項)&=&\int\int|C_1|^2φ^*_α(1)φ_α(1)φ^*_β(2)φ_β(2)d{\bf r}_1d{\bf r}_2\\&=&|C_1|^2\int φ^*_α(1)φ_α(1)d{\bf r}_1 \intφ^*_β(2)φ_β(2)d{\bf r}_2\\&=&|C_1|^2・1・1\\&=&|C_1|^2\end{eqnarray}
\begin{eqnarray}(第二項)&=&\int\int C^*_1φ^*_α(1)φ^*_β(2)C_2φ_α(2)φ_β(1)d{\bf r}_1d{\bf r}_2\\&=&C^*_1C_2\int φ^*_α(1)φ_β(1)d{\bf r}_1 \int φ^*_β(2)φ_α(2)d{\bf r}_2\\&=&C^*_1C_2・0・0\\&=&0\end{eqnarray}
\begin{eqnarray}(第三項)&=&\int\int C^*_2φ^*_α(2)φ^*_β(1)C_1φ_α(1)φ_β(2)d{\bf r}_1d{\bf r}_2\\&=& C^*_2C_1 \int φ^*_β(1)φ_α(1)d{\bf r}_1 \int φ^*_α(2)φ_β(2)d{\bf r}_2\\&=& C^*_2C_1 \int φ^*_β(1)φ_α(1)d{\bf r}_1 \int φ^*_α(2)φ_β(2)d{\bf r}_2\\&=&C^*_2C_1・0・0\\&=&0\end{eqnarray}
\begin{eqnarray}(第四項)&=&\int\int|C_2|^2φ^*_α(2)φ_α(2)φ^*_β(1)φ_β(1)d{\bf r}_1d{\bf r}_2\\&=&|C_2|^2 \int φ^*_β(1)φ_β(1) d{\bf r}_1 \intφ^*_α(2)φ_α(2)d{\bf r}_2\\&=&|C_2|^2・1・1\\&=&|C_2|^2\end{eqnarray}
以上より、求める規格化条件は、
$$1=|C_1|^2+|C_2|^2$$
対称関数の場合(ボーズ粒子)
\(Ψ(1,2)\)が対称関数
$$Ψ(1,2)=Ψ(2,1)$$
の場合、
$$C_1=C_2$$
となる。したがって、求める波動関数は、次のようになる。
$$Ψ(1,2)=\frac{1}{\sqrt{2}}[φ_α(1)φ_β(2)+φ_α(2)φ_β(1)]$$
このような波動関数をとる粒子をボーズ粒子とよぶ。
反対称関数の場合(フェルミ粒子)
一方、\(Ψ(1,2)\)が反対称関数
$$Ψ(1,2)=-Ψ(2,1)$$
の場合、
$$C_1=-C_2$$
となる。
したがって、求める波動関数は、次のようになる。
$$Ψ(1,2)=\frac{1}{\sqrt{2}}[φ_α(1)φ_β(2)-φ_α(2)φ_β(1)]$$
このような波動関数をとる粒子をフェルミ粒子とよぶ。
パウリの排他律とフェルミ粒子
パウリの排他律とは、同じ量子状態をとれるフェルミ粒子は1つのみというものである。これを、上の反対称の波動関数から考察する。
この排他律は、パウリ自身の研究結果を証明するために提唱された原理である。そのため、実験結果に合わせるためには、2つの粒子が同じ状態をとるときの波動関数を0と定義する必要がある。
両方の粒子が同じ状態\(α\)をとると仮定すると、反対称の波動関数\(Ψ(1,2)\)は、
\begin{eqnarray}Ψ(1,2)&=&\frac{1}{\sqrt{2}}[φ_α(1)φ_α(2)-φ_α(2)φ_α(1)]\\&≡&0\end{eqnarray}
となる。
おまけ スレイター行列
フェルミ粒子の波動関数をよく見ると、行列式に書き直せそうだ。
$$Ψ(1,2)=\frac{1}{\sqrt{2}}\begin{vmatrix} φ_α(1) & φ_α(2) \\ φ_β(1) & φ_β(2) \end{vmatrix}$$
このような行列式をスレイター行列とよぶ。この行列は、他の多粒子系にも応用可能であり、例えば3粒子系のフェルミ粒子の波動関数は、次のようになる。
$$Ψ=\frac{1}{\sqrt{3!}}\begin{vmatrix} φ_α(1) & φ_α(2) & φ_α(3) \\ φ_β(1) & φ_β(2) & φ_β(3) \\ φ_γ(1) & φ_γ(2) & φ_γ(3) \end{vmatrix}$$
まとめ
・2粒子系のシュレディンガー方程式から、ボーズ粒子とフェルミ粒子が満たす波動関数をそれぞれ求めた。
・フェルミ粒子の波動関数から、パウリの排他律を考察した。
参考文献
・村上雅人(2008)『なるほど量子力学III』,海鳴社.
・Eisberg, Robert Martin(1985) “Quantum physics of atoms, molecules, solids, nuclei, and particles,” New York : Wiley. 2nd ed.
(題名を斜体にできないので” “でくくっています)