フーリエ変換
$$F(k)=\int_{-∞}^{∞} f(x)e^{-ikx} dx$$
逆フーリエ変換
$$f(x)=\frac{1}{2π}\int_{-∞}^{∞} F(k)e^{ikx} dk$$
波が関数\(f(x)\)で与えられるとする。それをフーリエ変換すると、波\(f(x)\)を波数\(k\)の関数\(F(k)\)として表すことができる。\(F(k)\)は、\(f(x)\)に含まれる波を波数\(k\)ごとに分解して、それぞれの波の大きさを関数として表したものである。フーリエ変換すれば波\(f(x)\)を\(F(k)\)に変換できるし、逆フーリエ変換すれば\(F(k)\)を波\(f(x)\)に変形できる。
公式の覚え方
フーリエ変換は関数\(f(x)\)から変数\(x\)を追い出して\(F(k)\)を求める変換である。だから、フーリエ変換の公式では\(f(x)\)を\(dx\)で積分している。
逆フーリエ変換も同様に考える。これは、関数\(F(k)\)から変数\(k\)を追い出して\(f(x)\)を求める変換である。だから、逆フーリエ変換の公式では\(F(k)\)を\(dk\)で積分している。
フーリエ級数展開とフーリエ変換の違い
フーリエ級数展開は、波\(f(x)\)が周期的な関数のみ使えるものである。一方フーリエ変換は、波\(f(x)\)が周期性を持たない関数に使う。上の公式を見てもわかる通り、フーリエ変換の公式には、フーリエ級数展開の公式と違い、周期\(L\)が含まれていない。
また、フーリエ級数展開は展開後、波\(f(x)\)を正弦波の重ね合わせで表す。一方フーリエ変換は、\(F(k)\)を求めることで、波\(f(x)\)はどんな波数\(k\)の波を含むかや、\(f(x)\)に含まれる波数\(k\)の波の大きさがわかる。\(F(k)\)が連続ならば、このときの\(F(k)\)を連続スペクトルという。また\(F(k)\)が離散的ならば、このときの\(F(k)\)を離散スペクトルという。
例題
問題:次の関数をフーリエ変換せよ
テレビの白色の光をフーリエ変換すると
前に書いたフーリエ級数展開の記事では、テレビの白色光をフーリエ級数展開すれば光の三原色を表す波が求まると書いた。では、もし代わりにフーリエ変換するとどうなるだろうか。
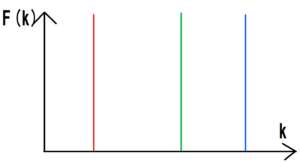
上の図は、テレビの白色光をフーリエ変換したときの結果の予想である。この図のように、赤・青・緑色を表す波数の周りの領域だけ大きなピークができるが、他の領域ではピークは存在しないだろう。赤い光ほど波長が長くなるため、波数\(k\)は小さくなるはずである。青い光は赤い光と逆で、波数\(k\)は大きくなる。
参考文献
・馬場敬之(2016)『スバラシク実力がつくと評判の演習 フーリエ解析 キャンパス・ゼミ』,マセマ出版社.

