系がした仕事を\(W’\)とおく。系Aがそれぞれの過程を経て系Bに至ったとき、次の式が成り立つ。
・定圧過程
一般的な気体:\(W’_{A→B}=p(V_B-V_A)\)
理想気体:\(W’_{A→B}=nR(T_B-T_A)\)
・等温過程
理想気体:\(W’_{A→B}=nRTln\frac{V_B}{V_A}\)
・断熱自由膨張
理想気体:\( \left( \frac{∂U}{∂V} \right) _T=0\)(ジュールの法則)
理想気体:\(C_p-C_V=nR\)(マイヤーの法則)
理想気体:\(dU=C_VdT\)
・断熱過程
理想気体:\(TV^{γ-1}=(定数)\)
理想気体:\(pV^γ=(定数)\)
目次
公式の導出
系Aの圧力、体積、温度をそれぞれ\(p_A\),\(V_A\),\(T_A\)、系Bの圧力、体積、温度をそれぞれ\(p_B\),\(V_B\),\(T_B\)とする。
定圧過程と系がした仕事\(W’\)
準静的過程において、系が受ける仕事\(W\)は次のようになった。
$$d’W=-pdV$$
参考:準静的過程とは
系がした仕事\(W’\)はこれにマイナスをつけたものだから、
$$d’W’=pdV$$
この式の両辺を体積で積分すればよい。\(p_A=p_B≡p\)とおく。
この\(W’_{A→B}\)は、体積が\(V_A\)から\(V_B\)に変化したときに気体がした仕事を表す。
したがって、
理想気体の状態方程式\(pV=nRT\)を\(T\)微分すると、\(p\),\(n\),\(R\)は定数であることに注意して、次の式を得る。
$$dV=\frac{nR}{p}dT$$
この式を、前の式の導出中の積分に代入する。
等温過程と系がした仕事\(W’\)
\(d’W’=pdV\)の体積積分に、理想気体の状態方程式\(p=\frac{nRT}{V}\)を代入すればよい。\(T_A=T_B≡T\)とおく。
\begin{eqnarray} W’_{A→B}&=&\int_{V_A}^{V_B} \frac{nRT}{V} dV\\&=&nRTln\frac{V_B}{V_A} \end{eqnarray}
断熱自由膨張における公式
自由膨張の実験とジュールの法則
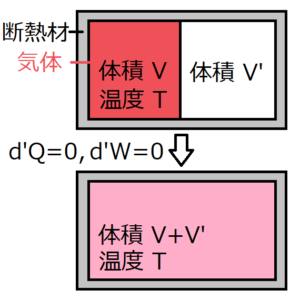
上のように、断熱材付きの容器の中に仕切りを入れて、片側の部屋にだけ気体を入れる。この状態から仕切りを取り除き、十分時間が経って平衡状態になる過程を考える。ジュールによって、仕切りを取り除く前と後では温度\(T\)は変わらないという実験結果が得られた。さらに、この系には外部から熱と仕事の出入りがないため、熱力学第一法則より、内部エネルギーの変化も0である。実験結果をまとめると、体積が変化しているにもかかわらず、内部エネルギーも温度も変化していないということになる。
この実験結果から、温度を一定とすると、断熱過程における理想気体の内部エネルギー\(U\)は、体積\(V\)に依存しないことがいえる。
ちなみにこの現象を断熱自由膨張といい、この実験をジュールの実験と呼ぶ。
マイヤーの法則
定圧熱容量\(C_P\)の式にジュールの法則を代入すると、次のようになる。
参考:定積熱容量と定圧熱容量
理想気体の状態方程式\(V=nRT/p\)を代入する。
$$C_P=C_V+nR$$
\(dU=C_VdT\)の導出
内部エネルギーの微小量\(dU\)を次のように表す。
ジュールの法則を適用すると、
ここで、\(\left( \frac{∂U}{∂T} \right)_V\)は定積熱容量\(C_V\)であったことを思い出す。
$$dU=C_VdT$$
断熱過程における公式
\(TV^{γ-1}=(定数)\)の導出
熱力学第一法則に\(d’Q=0\)(断熱)を代入する。気体が受けた仕事を\(d’W\)とすると、
$$dU=d’W=-pdV$$
\(dU=C_VdT\)と\(p=nRT/V\)を代入すると、
マイヤーの公式を使うと、\(nR=C_p-C_V\)より、
両辺を\(C_VT\)で割る。
ここで、比熱比\(γ\)を次のように定義する。
$$γ≡\frac{C_p}{C_V}$$
この比熱比\(γ\)を使うと、
両辺を積分すると、
\(AlnB=lnB^A\)と\(lnA+lnB=lnAB\)を思い出すと、
$$lnTV^{γ-1}=(定数)$$
以上より、次の式が求められた。
$$TV^{γ-1}=(定数)$$
\(pV^γ=(定数)\)の導出
\(TV^{γ-1}=(定数)\)に理想気体の状態方程式\(T=\frac{pV}{nR}\)を代入すればいい。\(nR\)は右辺の定数項にまとめられるから、求めたい式が導出できる。
$$pV^γ=(定数)$$
等温過程と断熱過程グラフ
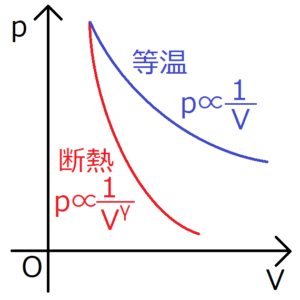
断熱変化の公式\(pV^γ=(定数)\)を変形すると、圧力\(p\)と\(V^γ\)が反比例の関係にあることがわかる。
一方の等温過程では、\(pV=(一定)\)より、圧力\(p\)と\(V\)が反比例の関係にある。
比熱比\(γ\)は1より大きいから、図にあるように、断熱過程のグラフの方が傾きが急になる。このことはカルノーサイクルを考える上で非常に重要となる。
参考文献
・三宅哲(1994)『熱力学』,裳華房.

