潜熱とは、相Aから相Bに相転移するときに、系に出入りする熱のことである。この記事では、なぜ相転移に潜熱がつきものなのかを考える。
温度変化による相転移
ギブスの自由エネルギーと相転移の向き
物質量\(N\)mol、圧力\(p_0\)の系を考える。この系において、系の相がすべて相Aから相Bに変化したときのギブスの自由エネルギーの変化は、次のようになる。
上の式から、\(μ_A<μ_B\)ならば\(G_A<G_B\)が成り立ち、また\(μ_A>μ_B\)ならば\(G_A>G_B\)が成り立つ。このことと、化学ポテンシャルが小さい方向に相転移が進むことを考慮すると、ギブスの自由エネルギーが小さい相に向かって相転移が発生するといえる。
ギブスの自由エネルギーの傾き
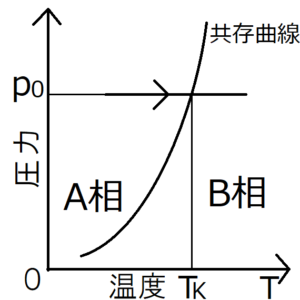
圧力\(p_0\)下で系の温度を上昇させることで、相Aから相Bへ相転移した場合を考える。ただし、相転移が発生する温度を\(T_K\)とする。上の相図よりこの系は、温度が\(T_K\)より小さければ相A、大きければ相Bをとることがわかる。これに注意して、それぞれの相のギブスの自由エネルギー\(G_A,G_B\)と温度\(T\)のグラフを描くと、次のようになる。
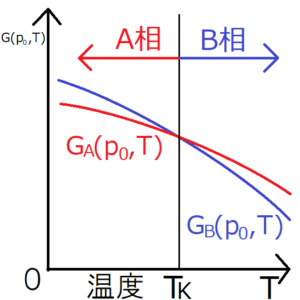
相転移が起こるためには両方のギブスエネルギーのグラフが交差しなければならないため、両グラフの傾きは一般には異なる。
相転移によるエントロピー変化
等圧(\(dp=0\))におけるギブスの自由エネルギーの変化分\(dG\)は、次のようになった。
この式の両辺を\(dT\)で割ると、\(G\)の\(t\)偏微分がエントロピー\(S\)にマイナスをつけたものと等しくなることがわかる。
ここで、G-Tグラフにおける\(G_A\)と\(G_B\)に注目すれば、\(G_B\)のほうが\(G_A\)より傾きが小さいことがわかる(両グラフとも負の傾きを持っているため、垂直に近いほうが傾きが小さいことになる)。
相Aと相Bのエントロピーをそれぞれ\(S_A,S_B\)とおいて、上の式に代入する。
両辺にマイナスをかけると不等号の向きが逆になるから、
この式から、相Bのエントロピーのほうが、相Aのものよりも大きいことがわかる。
エントロピー変化と潜熱
可逆変化を前提とすると、熱\(d’Q\)と温度\(T\)、エントロピー変化\(dS\)の間には次の関係式が成り立つ。
参考:エントロピーの定義とは
今考えている相転移においては\(dS=S_B-S_A\)だから、これを代入すると、
この式は、相Aから相Bに相転移するとき、熱\(d’Q\)を系に与える必要があることを意味する。この相転移に必要な熱のことを潜熱という。
以上より、相転移に潜熱が必要な理由は、熱を入れて系のエントロピーを\(S_A\)から\(S_B\)まで上げることで、ギブスエネルギーのグラフの\(G_A\)から\(G_B\)への乗り換えを行う必要があるためだといえる。
相転移が発生する温度\(T_K\)と潜熱は、物質によって異なる値をとる。潜熱は、1gあたりの物質の相転移に必要なエネルギーという形で表される。例えば氷が水に相転移する温度は273.15Kで、潜熱は334J/gである。
まとめ
・相ごとのG-Tグラフの傾きから、相転移によるエントロピー変化を考えた。
・相転移に潜熱が必要な理由を考えた。
参考文献
・三宅哲(1994)『熱力学』,裳華房.

