ケプラーの法則とは、惑星の運動に関する法則である。この法則を使いこなせるようになれば、惑星の運動を簡単に考えることができる。そして、これについて考えるには2次元の極座標の運動方程式を導入するのが一番手っ取り早い。この記事では、ケプラーの法則の紹介と、その証明を行う。
目次
2次元の極座標の運動方程式
動径方向成分の運動方程式
$$F_r(t)=m\left( \ddot{r}-r\dot{φ}^2\right)$$
角度方向成分の運動方程式
$$F_φ(t)=m\left( 2\dot{r}\dot{φ}+r\ddot{φ} \right)$$
数式を見やすくするために、物理では時間微分を、変数の上にドットをつけて\(\dot{r}\)と表すことが多い。
ケプラーの法則
ケプラーの第一法則(楕円軌道の法則)
惑星は、太陽を焦点の一つとする楕円軌道上を動いている。
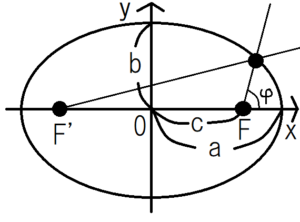
極座標で楕円を表すと、次のようになる。
$$r=\frac{l}{1+εcos{φ}}$$
\(ε=\frac{c}{a}\):離心率 \(l=\frac{b^2}{a}\):半直弦
ケプラーの第二法則(面積速度一定の法則)
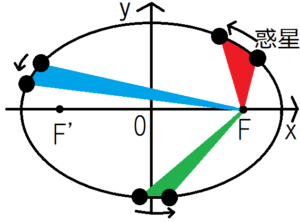
惑星の中心と楕円軌道の焦点\(F\)を線で結ぶ。この線が単位時間で描く面積は一定である。上の図を使って言い換えると、赤・青・緑の面積はすべて等しくなる。
ケプラーの第三法則(調和の法則)
惑星の公転周期の2乗は、楕円軌道の長半径\(a\)の3乗に比例する。
$$T^2∝a^3$$
例題1 第一法則の証明
万有引力について
万有引力とそれによるポテンシャルは次のように表される。
$$f(r)=-G\frac{mM}{r^2}$$
$$U(r)=-G\frac{mM}{r}$$
ここで、\(m\)は惑星の質量、\(M\)は太陽の質量である。
角度方向の運動方程式
まずこの系では、惑星に働く角度方向の力は\(0\)である。
$$m\left( 2\dot{r}\dot{φ}+r\ddot{φ} \right)=0…(1)$$
また部分積分に気を付けると、次の式が成り立つことに注意する。
式(2)の右辺は、式(1)の両辺に\(\frac{r}{m}\)をかけただけのものだから、
$$\frac{d}{dt}(r^2\dot{φ})=0$$
両辺を\(t\)で積分すると、tに依存しない定数\(h\)使って、次の式を得る。
$$r^2\dot{φ}=h…(3)$$
この式(3)はこの後何度も出てくるので、常に頭に入れておくように。
距離\(r\)を角度\(φ\)で表すには
式(3)を利用して、距離\(r(t)\)の時間微分\(dr/dt\)を角度\(φ(t)\)に関する微分\(dr/dφ\)に変換する。
\(u=\frac{1}{r}\)とおくと\(du=-\frac{dr}{r^2}\)だから、
$$\frac{dr}{dt}=-h\frac{du}{dφ}$$
この式をまた\(t\)で微分する。
動径方向の運動方程式
今までの結果を、下の動径方向の運動方程式に代入する。
\(F_r(t)\)には万有引力\(-G\frac{mM}{r^2}\)、\(\ddot{r}\)には先ほど考えた式、\(\dot{φ}\)には式(3)を入れればよい。
この式の両辺に\(\left( -\frac{r^2}{h^2m} \right)\)をかけて、\(u=\frac{1}{r}\)を代入する。
あとはこの微分方程式を解けば\(u(φ)\)が求まり、そこから\(r\)も求められる。
微分方程式の解き方
式(4)のような微分方程式を解くには、まず変数\(u\)を含まない項を\(0\)としたときの解を求めればよい。つまり、最初に次の方程式を解く。
$$\frac{d^2u}{dφ^2}=-u$$
この微分方程式は単振動のものと同じ形をしているため、解\(u(φ)\)は、初期位相\(φ_0\)と定数\(A\)を使うと次のように表せる。
$$u(φ)=Acos(φ-φ_0)$$
このようにして得られた解を、斉次方程式の一般解という。
さらに、\(u(φ)=\frac{GM}{h^2}\)とすることでも、式(4)を満たす。この\(u(φ)\)は、非斉次方程式の特解という。
式(4)の一般解は、斉次方程式の一般解と非斉次方程式の特解の和となる。
\(u=\frac{1}{r}\)を代入すれば、ようやく求めるべき方程式が出てくる。
ここで、\(l=\frac{h^2}{GM}\)、\(ε=\frac{h^2}{GM}A\)とおいた。\(φ_0\)は長軸方向を表す。
この\(r(φ)\)は、\(ε\)の値によって表される図形が変わる。\(ε=0\)なら円、\(0<ε<1\)なら楕円、\(ε=1\)なら放物線、\(ε>1\)ならば双曲線である。
例題2 第二法則の証明
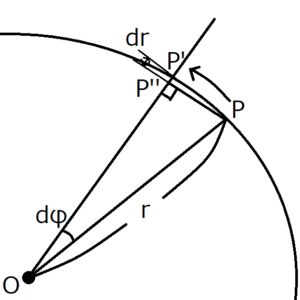
上のように、惑星が\(P\)から\(P’\)まで動いたとする。このときの面積速度は\(OPP’\)である。\(OPP’\)を求めて、これがtに依存しない定数であることを示せばよい。
\(P\)から直線\(OP’\)の垂線を引き、垂線と\(OP’\)の交点を\(P”\)とおく。
角度\(dφ\)が小さいとき、\(PP”=rdφ\)と近似できる。すると面積速度\(OPP’\)は次のようになる。
\(dr\)と\(dφ\)は十分小さいとする。そしたら、その両方を含む第二項は、第一項と比べて十分小さいとみなせるため、第二項を無視できる。
$$OPP’≒\frac{1}{2}r^2dφ$$
面積速度を求めるには、面積\(OPP’\)を時間\(dt\)で割ればよい。
最後に例題1の式(3)を使った。\(h\)はtに依存しない定数だから、面積速度は一定であるといえる。
例題3 第三法則の証明
半直弦の定義より、\(b=\sqrt{al}\)。例題1の最後の\(l=\frac{h^2}{GM}\)より、\(h=\sqrt{GMl}\)となる。
周期\(T\)をもとめるには、楕円の面積\(πab\)を面積速度\(\frac{h}{2}\)で割ればよい。
両方を二乗すれば、求めたい関係がでる。
$$T^2∝a^3$$
参考文献
・戸田盛和(1982)『力学 〔物理入門コースI〕』,岩波書店.

