[mathjax]
目次
ニュートンの運動の第1法則(慣性の法則)
物体に働く力がつり合っていたり、全く力が働いていない場合、その物体は静止し続けるか、等速直線運動をする。
ニュートンの運動の第2法則(運動方程式)
力\({\bf F}\)、物体の質量\(m\)、物体の位置\({\bf r}(t)\)は次の関係を満たす。
ニュートンの運動の第3法則(作用反作用の法則)
物体Aが物体Bに力を与えるとき、物体Bも物体Aに対して、その力と同じ大きさかつ逆向きの力を与える。
ニュートンの運動の第1法則(慣性の法則)
慣性の法則は、物体に力が働いていないか、力がつり合っているとき、その物体は前の運動状態を維持するという内容であった。もし力が働かなくなったりつり合ったりする直前で、物体が静止していたら、その物体は静止し続ける。逆に速度\({\bf v}\)で動いていたら、物体は速度\({\bf v}\)で等速直線運動をし続ける。
つり合いの式
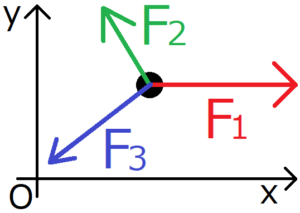
上の図は、2次元座標上の黒い質点に3つの力がかかっている様子を表している。まずはそれぞれの力のx軸方向の成分に注目してみる。図より、力\({\bf F}_1\)のx成分は正だが、\({\bf F}_2,{\bf F}_3\)は負であることがわかる。y軸方向の力にも同様にして注目すると、\({\bf F}_1\)は\(0\)だが、\({\bf F}_2\)は正、\({\bf F}_3\)は負の方向を向いている。このように、力\({\bf F}\)は、その向きによって正になることもあれば負になることもある。だから、この力の和が正と負で打ち消しあうことで、質点にかかる力が全体で0になるということもあり得る。この打ち消しあって\(0\)になった状態を、力がつり合っている状態という。
力が働かないか、つり合っているという状況を数式で表すと、次のようになる。
$$\displaystyle \sum_i {\bf F}_i=0$$
ニュートンの運動の第2法則(運動方程式)
高校では加速度\(a\)を使って、\(F=ma\)という運動方程式を考えた。だが、加速度\(a\)は速度\(v\)の時間微分であり、また速度\(v\)は位置\(r\)の時間微分である。したがって、加速度\(a\)は位置\(r\)の二階微分となる。
だから、力\({\bf F}\)を位置\({\bf r}\)の二階微分を使った式で表せる。
同じ大きさの力\(F\)を与えた場合、物体の質量\(m\)が大きいほど、加速度を与えにくくなる。したがって、質量\(m\)は、物体の動きにくさを表す指標と言い換えることができる。
また、運動量\({\bf p}=m{\bf v}\)を導入すると、質量は時間変化しないから、力\({\bf F}\)は\({\bf p}\)の時間微分と等しいと言い換えができる。
ニュートンの運動の第3法則(作用反作用の法則)
物体Aが物体Bに力を与えるとき、物体Bも物体Aに対して、その力と同じ大きさかつ逆向きの力を与える。
この法則の例としては、垂直抗力が有名である。
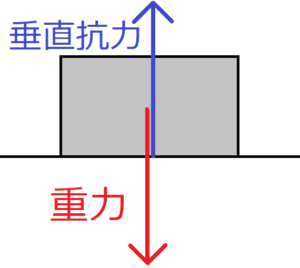
机の上に置いてある物体が、重力で下方向に引っ張られている。このとき、物体は机を押しているが、それと同時に机もまた物体を押し返している。この押し返す力を垂直抗力という。
この垂直抗力は2つのものが接触しないと発生しないが、接触していない力でも作用反作用の法則は成り立つ。
スカイダイビングから考える質量の意味
質量が物体の動きにくさを表すことを、スカイダイビングを例に考えてみる。
ヘリコプターから飛び降りた人は、当然地球の重力によって下に落ちていく。それと同時に、作用反作用の法則より、人もまた、重力と同じ大きさで地球を引き寄せている。ところが実際は、両方の力が同じにもかかわらず、人が地球に吸い寄せられるばかりで、地球のほうが公転軌道からずれて人に向かってくるようなことはない。
なぜならば、地球の質量のほうが、人の質量よりもはるかに大きいからである。人の質量を\(m\)、地球の質量を\(M\)とおくと、人にかかる力\(F_m\)と地球にかかる力\(F_M\)は、作用反作用の法則と万有引力の式より、次のようになる。
この力をもとに、地球と人それぞれの運動方程式をつくる。
両方の式を整理すると、
左辺はそれぞれの加速度を表している。そして両式の右辺に注目すると、人の加速度は地球の質量\(M\)、地球の加速度は人の質量\(m\)を分数の分子に含むことがわかる。だから、人の加速度の方が圧倒的に大きい。
以上をまとめると、同じ大きさの力が働いているにもかかわらず、質量が小さい人間のほうが、質量が大きい地球よりも大きい運動をする。こう考えれば、質量が物体の動きにくさを表す指標ということも納得しやすいだろう。
おまけ
この\(G\)は万有引力定数であり、次のように定義される。
この値と地球の質量\(M\)、地球の半径\(r\)を、上の人の加速度を表す式に代入すれば、重力加速度\(g≒9.8\)が求まる。実際に調べて求めてみよう。スカイダイビングの高度は、地球の半径と比べたら十分小さいため、無視できる。
まとめ
・3つのニュートンの運動の法則を確認した。
・スカイダイビングを例に、質量が物体の動きにくさを表すことを確認した。
参考文献
・都築嘉弘(2005)『チャート式シリーズ 新物理II』,数研出版.
・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

