[mathjax]
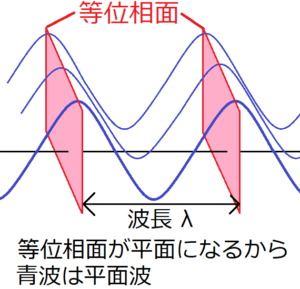
上の図では、同形の青い波が、奥にも複数存在する様子を表している。このような波では等位相面は平面になるため、図中の青い波は平面波と呼ばれる。
等位相面とは、同じ位相の場所を通り、かつ波の進行方向に対して垂直になるような面のことである。上の図では、波の頂上を通るような等位相面を赤い平面で表している。
この記事では、波動方程式から平面波を導出する。
目次
次元ごとの平面波の式
一次元の平面波の式
\(A\):振幅 \(k\):波数(単位長さあたりの波の数) \(ω\):角振動数
三次元の平面波の式
\({\bf k}\):波数ベクトル(波の進行方向を向く)
この波の式は、波数ベクトルの方向に、一定の間隔で波が現れることを表している。
波動方程式と平面波の数式
波動方程式は、変位を\(ψ\)とすると、次のように書ける。
参考:波動方程式を弦の振動から導出してみた
この右辺を移項して、因数分解する。
左辺の2つのカッコ内のどちらかが0ならば、等式が成立する。
関数\(ψ\)の変数について、式(2)は\(ψ=f(x-vt)\)、式(3)は\(ψ=g(x+vt)\)とおけば、それぞれの式を満たす。したがって、波動方程式の一般解はこれらの和で表されるから、一般解\(ψ(x,t)\)は次のように書ける。
\(f(x-vt)\)は速さ\(v\)でx軸方向に進む波、\(g(x+vt)\)は速さ\(v\)でx軸とは逆方向に進む波を表している。
関数\(f(x-vt)\)と\(g(x+vt)\)の例
波動方程式を満たす関数の例として、複素定数\(\hat{A}\)を使った次の式が挙げられる。
この式(4)の右辺は変数\((x-vt)\)を含んでいるため、\(f(x-vt)\)に対応する。式(4)を波動方程式である式(1)に代入すれば、式(4)が波動方程式を満たすことを確認できる。
これに加えて、次の関係を導入する。
このような角振動数\(ω\)と波数\(k\)の関係式を、分散関係という。上の式は平面波の分散関係を表している。この角振動数を式(4)に代入する。
後は関数\(ψ(x,t)\)の実部をとると、よく見る三角関数を使った波動関数の式が求まる。
三次元の平面波の式
式(1)は\(x\)軸についての波動方程式であるが、この波動方程式は\(y\)軸と\(z\)軸でも同様に成り立つ。
すべての軸における波動方程式をまとめると、位置ベクトル\(\bf r\)を使った3次元の波動方程式が求まる。
この3次元の波動方程式について、\(x\)軸の波動方程式と同じように考えると、3次元の波動関数が求まる。
ここで、\(\bf k\)は波数ベクトルである。
波数ベクトルの成分\(k_x,k_y,k_z\)は、それぞれx軸、y軸、z軸における波数である。
式(5)の波動関数の実部をとると、
まとめ
・等位相面と平面波の説明をした。
・平面波の波動関数を考えた。
参考文献
・長谷川修司(2009)『講談社基礎物理学シリーズ2 振動・波動』,講談社.

