1. /
  2. /
  3. 力積と運動量の関係

力積と運動量の関係

  • このエントリーをはてなブックマークに追加
  • LINEで送る

力積とは、時間\(Δt\)の間に、力\({\bf F}\)が物体に与える運動量のことである。数式では、次の式の左辺のような形をとる。

$${\bf F}･Δt={\bf p}(t_0+Δt)-{\bf p}(t_0)･･･(1)$$

この記事では、まず力積のイメージをF-tグラフでつけた後、壁がボールに与える力積を求める。

力積とは

グラフから考える力積のイメージ

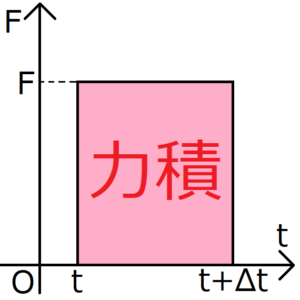
上の図は、力\({\bf F}\)と時間\(t\)のグラフを表している。力積は\({\bf F}･Δt\)で定義されるから、力積は\(F-t\)グラフの面積だと言い換えができる。

もし\(F-t\)グラフが長方形でなかったら

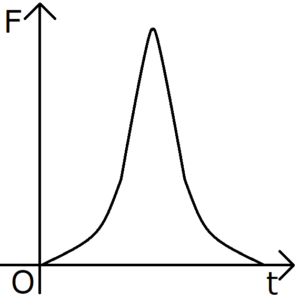
式(1)で表される力積の式は、高校生向けの微積分を使わない形となっている。ところが現実の\(F-t\)グラフは、上図のように長方形にはなっていないことが多いため、式(1)の力積の式では対応できない。例えば下のボールが壁にぶつかる問題でも、実際には上のグラフのように、ボールに瞬間的に強い力がかかるのであって、一定の力が時間\(Δt\)だけかかるというわけではない。

そこで、次の図のように、グラフが作る面積を、細さが無限小\(dt\)の長方形で分割して近似してみる。細さが無限小ということは、グラフの横軸は時間\(t\)だから、\(dt \to 0\)の極限をとればよい。

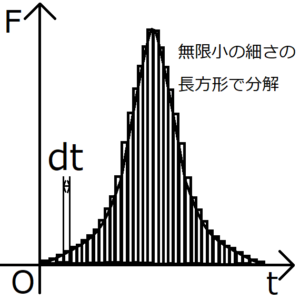
この図から、無限小の細さの長方形の面積の総和が、求める力積となることがわかる。細い長方形の辺の長さはそれぞれ縦\({\bf F}\)横\(dt\)だから、その面積は\({\bf F}･dt\)となる。

運動方程式から力積を求める

運動量を使ってニュートンの運動方程式を書く。

$${\bf F}=\frac{d{\bf p}(t)}{dt}$$

参考:ニュートンの運動の法則と質量の意味

この式の両辺に\(dt\)をかけて、両辺を積分する。

$$\int_{t_0}^t {\bf F}dt={\bf p}(t)-{\bf p}(t_0)$$

この式の左辺が、力積を積分で表したものとなる。これで、力\({\bf F}\)が時間\(t\)に依存する関数で表現できれば、力のグラフの形にかかわらず、その力積も求められるようになった。

例題 壁がボールに与える力積

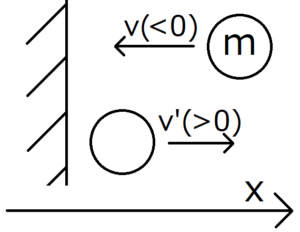
質量\(m\)のボールが、図のように速度\(v\)で壁に向かっている。x軸の方向と\(v\)の向きは逆だから、この\(v\)は負になる。そして壁に跳ね返された後、ボールは速度\(v’\)で運動する。このときに壁がボールに与えた力積を求めたい。

壁に衝突する前のボールの運動量は\(mv\)、衝突後の運動量は\(mv’\)である。

衝突の前後の運動量の変化分が、壁がボールに与えた運動量、つまり力積となる。だから求める力積は、衝突後の運動量から衝突前の運動量を引けば求められる。

\begin{eqnarray} F･Δt&=&p_{衝突後}-p_{衝突前}\\&=&mv’-mv\\&=&m(v’-v) \end{eqnarray}

\(v<0\)より、もし\(|v’|=|v|\)ならば、力積は次のようになる。

$$F･Δt=m(v’-(-v’))=2mv’$$

まとめ

・力積の意味と定義を確認した。

・衝突前後のボールの速度の変化から、壁がボールに与える力積を求めた。

参考文献

・都築嘉弘(2005)『チャート式シリーズ 新物理II』,数研出版.

・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

  • このエントリーをはてなブックマークに追加
  • LINEで送る

SNSでもご購読できます。

コメントを残す

*

CAPTCHA