速度に比例する空気抵抗の例は意外と身近に存在するが、その一つが雨粒である。今回は、比較的簡単な速度に比例する空気抵抗を見てみる。
落下速度の求め方
運動方程式の導出
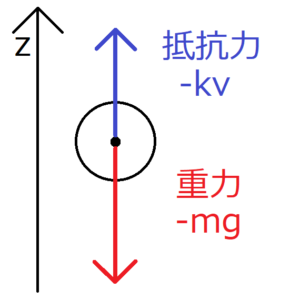
落下している雨粒には、重力と、重力とは反対方向の抵抗力が働く。上向きにz軸を設定すると、重力はz軸とは逆方向に働くから符号は負、抵抗力は常に速度\(v\)とは逆方向に働くから符号は負になる。これに注意して運動方程式を書く。ただし、\(k\)を比例定数とする。
運動方程式の解き方
まず両辺を\(m\)で割って、左辺を微分のみにする。
次に\(v\)を左辺にまとめたい。ただし、単純に両辺を\(v\)で割るだけでは\(-g\)の項に\(v\)が残ってしまう。そこで、右辺を\(v\)の係数でくくることで、(vを含まない数)×(vを含む数)という形をつくる。今の例では、(\(v\)を含まない数)が\(-k/m\)、(\(v\)を含む数)が\((v+(mg/k))\)となる。
後は両辺を(\(v\)を含む数)で割れば、\(v\)を左辺にまとめられる。
両辺に\(dt\)をかける。
両辺の積分をとる。
左辺の積分
確認だが、\(C_1\)は積分定数、\(ln\)はネイピア数\(e\)を底とした対数である。つまり、\(ln\)は\(log_e\)とも書ける。
右辺の積分
\(C_2\)は積分定数である。
以上をまとめると、次の式を得る。
ただし、積分定数は\(C_3=C_2-C_1\)としてまとめた。
両辺の指数をとると、次のようになる。
ここで、\(e^{lna}=a\)に気をつけると、
左辺の絶対値を外すと、
\(v\)について整理すると、
ただし、\(C=\pm e^{C_3}\)とおいた。
初期条件の検討
初期条件を導入することで、比例定数\(C\)を求める。
雨粒は時刻\(t=0\)で落下し始めるとする。
\(t=0\)で\(v(0)=0\)より、
最終的な\(v(t)\)のグラフは、次のようになる。
グラフ化
求めた速度\(v(t)\)をグラフ化する。\(e^{-\frac{k}{m}t}\)のグラフを想像してからだとグラフを描きやすい。
\(t→∞\)で\(e^{-\frac{k}{m}t}→0\)になることに注意する。
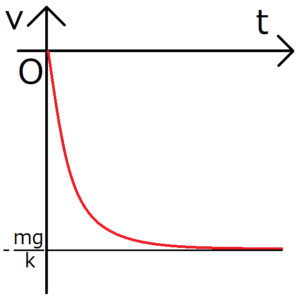
このグラフから、十分時間が経過すると、雨粒の速度が収束することがわかる。今回の場合、速度は\(-\frac{mg}{k}\)に収束するが、このときの速度を終端速度という。
速度が一定になるということは、雨粒にかかっている力が釣り合っていることを意味する。つまり、雨粒が終端速度で落下しているときは、雨粒に働く重力と抵抗力が釣り合っている。
雨粒以外の例
今回は雨粒の運動に注目したが、似たような計算で求められるものもある。
例えば、RL直列回路(抵抗とコイルを直列につないだ回路)に直流電圧をかけたときの電流を求める計算は、雨粒の速度の計算に似ている。
導体中を流れる電子の速度は、その速度に比例する抵抗力が速度とは逆向きに電子にかかると近似することで、雨粒の落下運動と同様にして求めることができる。
まとめ
・落下する物体が速度に比例する空気抵抗を受けるとき、十分時間がたつと、その速度は終端速度に収束する。
参考文献
・副島雄児・杉山忠男(2009)『講談社基礎物理学シリーズ 1 力学』,講談社.

