
今回のコラムのテーマは、「量子コンピュータ」です。
2017年11月20日、NTTが一般向けの国産の量子コンピュータを使ったシステムを発表しました。最近よく量子コンピュータという単語を耳にしますが、これは普通のコンピュータとは何が違うのでしょうか?この記事では、量子コンピュータと従来のコンピュータの違いや、量子コンピュータに使われる量子ドットについて、簡単に触れていきたいと思います。
目次
普通のコンピュータとは
量子コンピュータに触れる前に、まず普通のコンピュータについて説明します。
普通のコンピュータは、「0」と「1」という二種類の信号のみで動いています。少なからずネットを利用したことがある方ならば、一度は聞いたことがあると思います。一般的に「0」とは電位が低い状態、「1」とは電位が高い状態をいいます。この二種類の記号を使って計算する方法を、二進法といいます。
量子コンピュータと従来のコンピュータの違い
普通のコンピュータは「0」と「1」を最小単位として計算するのに対し、量子コンピュータは量子メモリと呼ばれるものを最小単位として計算します。この量子メモリにいくつかの量子ドット(量子ビット)が入っています。
従来の計算方法で用いていた電位の高低と、量子メモリの決定的な違いは、1つの最小単位で表せる状態の数が異なることです。具体的には、電位の高低だと「0」と「1」の2通りしか表現できませんが、量子ドットを使う場合、1つの量子メモリで\(2^n\)通りの状態を表現できます。
なぜ量子メモリはたくさんの状態を表せるのか
量子ドットの正体は、量子レベルに小さい粒子です。例えば、電子や原子核が挙げられます。それらの中で、今回は電子について考えます。この電子に情報を載せるために、電子の2つの状態をそれぞれ「0」と「1」に割り当てる必要があります。例えば、電子のスピンという状態を「0」と「1」に割り当てる場合、それぞれ「下向きのスピン」と「上向きのスピン」という状態に割り当てることができます。
電子のスピンとは何か
高校まででは学習しないことですが、実は電子は角運動量の次元を持つパラメータをもっています。角運動量の次元を持っているからといって、電子が自転しているというわけではないので注意してください(ただしここでは簡単のため、自転しているものと仮定します)。
そして、このスピンには、「下向きのスピン」と「上向きのスピン」とよばれる2種類があります。この向きは、スピンの回転方向を親指以外の指の向きに、スピンの向きを親指の向きに見立てた右ねじの方向に対応しています。
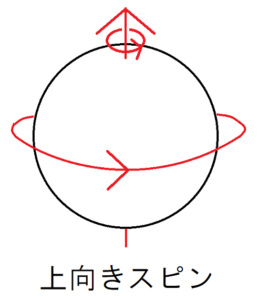
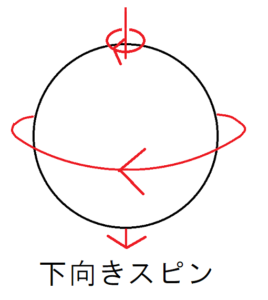
電子は粒子であり、波でもある
電子などの小さい物体は、粒子と波の両方の性質を持っています。波の性質をもつということは、重ね合わせの原理より、電子の状態を重ね合わせで表現できることを意味します。この性質を使うと、電子のスピンすらも、重ね合わせで表現することができます。スピンの重ね合わせを考えると、「電子が左回りで回っていてなおかつ右回りでも回っている」という状態が現れます。普通に考えて矛盾するようなことでも、量子レベルの世界では当たり前のことなのです。(ちなみに人間が「左回りで回っていてなおかつ右回りでも回っている」状態の電子を観察すると、その瞬間状態の重ね合わせが壊れて、電子が右回りか左回りのどちらかをするようになります。)
ちなみに、スピンの重ね合わせを数式を用いて表すと、次のようになります。
量子メモリがたくさんの状態を表せる理由
量子メモリがたくさんの状態を表せる理由のキーワードは、電子の状態の重ね合わせです。上の数式で例えると、\(|a>\)を検出できたら、同時に\(α\)と\(β\)が求まります。
量子メモリに1つの量子ドットの場合
例えば、次のスピンをもった電子が観測されたとします。
この式を、前の\(α\)や\(β\)を含むベクトルの方程式の左辺に代入すると、観測された電子は、下向きのスピン0と上向きのスピン1の重ね合わせになっていることがわかります。
以上の作業から、1つの量子ビットを観測するだけで、「下向きのスピン」と「上向きのスピン」という2種類の電子の状態を知ることができました。
量子メモリ中の量子ドットを増やした場合
高校で学習した場合の数を思い出しましょう。表裏が区別できるコインをn回投げたとき、その場合の数は\(2^n\)となりました。
このことを踏まえて、次に量子ドットの数を2つ観測した場合を考えましょう。観測する量子ドットを2つにすると、電子は2つの状態をもつため、全部で\(2^2=4\)つの状態を表せます。3つの量子ドットを観測すれば\(2^3=8\)つの状態、4つの量子ドットでは\(2^4=16\)の状態を表せます。したがって、1つの量子メモリ当たりの量子ドットを\(n\)とする場合、1つの量子メモリに記憶できる状態の数は\(2^n\)となります。最初に、1つの量子メモリで\(2^n\)通りの状態を表現できると書いたのは、このためです。
量子コンピュータは、この状態の重ね合わせを利用して、大量の数式を同時に計算することができるのです。
量子コンピュータのメリット
では、量子ドットを使う利点は何でしょうか。実は、「0」と「1」のみを使う従来のコンピュータが苦手としている計算というものも多いのです。例えば、200桁の因数分解を従来のコンピュータで計算すると、10年かかると言われています。1万桁になると1000億年になり、全く実用的ではありません。ところが、量子コンピュータを使えば、200桁の因数分解は数分、1万桁でも数時間から数日で終わります(参考文献1,p.25より)。つまり、従来のコンピュータでは時間がかかりすぎてできない計算ができることが、量子コンピュータのメリットなのです。
まとめ
・量子コンピュータは、量子メモリと呼ばれる最小単位を用いて計算する。
・量子コンピュータは、従来のコンピュータでは計算できないものでも計算できる。
以上です。ただし、この記事に書かれていることは、量子コンピュータのほんの入り口にすぎません。さらに詳しく知りたい方は、下の参考文献を図書館などでご覧になってみてください。どちらの本も、前提知識がほとんどない状態でも理解しやすいのでおすすめです。
参考文献
1.竹内繁樹(2005)『量子コンピュータ 超並列計算のからくり』,講談社.
2.西野哲朗(2007)『図解雑学 量子コンピュータ』,ナツメ社.
3.日本電信電話株式会社(2017)「NTT HOME > NTT持株会社ニュースリリース > 量子ニューラルネットワークをクラウドで体験」,(http://www.ntt.co.jp/news2017/1711/171120a.html),最終アクセス日2017/11/22.



