[mathjax]
座標系\(S\)に対して、座標系\(S’\)が速度\(\bf V\)で等速平行移動している場合を考える。この場合、座標系\(S\)が慣性系ならば、座標系\(S’\)も慣性系となる。このことをガリレイの相対性原理という。この記事では、この原理の証明を行う。
目次
「Bに対するAの速度」とは
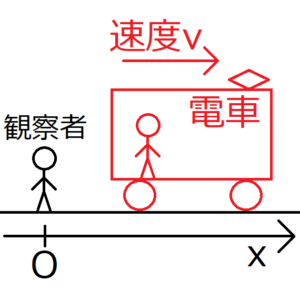
図のように、観察者\(O\)から速度\(+v\)で離れる電車が存在する。
観察者からみれば、当然電車は速度\(+v\)で進んでいるように見える。この場合、観察者に対する電車の速度は\(+v\)だという。
ところが電車から観察者をみると、観察者は速度\(-v\)で動いているようにみえるだろう。事実、電車に乗っていると、電車と同じ速度で周りの景色が後ろに流れていく。この場合、電車に対する観察者の速度は\(-v\)だという。
このように、「Bに対するAの速度」は、「Bから観察したときのAの速度」と言い換えることができる。このように、一方から見た他方の速度のことを、相対速度とよぶ。
慣性系・慣性力とは
座標系の設定
慣性系とは、ニュートンの運動法則が成立するような座標系を指す。
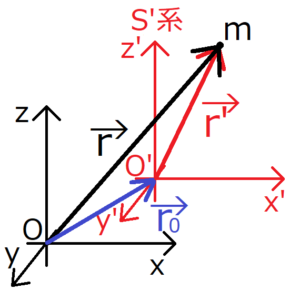
座標系\(S\)に対して、座標系\(S’\)が速度\(\bf V\)で平行移動している。系\(S\)における系\(S’\)の原点の位置を\({\bf r}_0\)とする。そして、系\(S’\)における質点\(m\)の位置を\({\bf r}’\)とする。すると、系\(S\)における質点の位置\({\bf r}\)は、\({\bf r}_0\)と\({\bf r}’\)の和で表される。
この3種類の位置はすべて時刻\(t\)のみに依存する関数だから、後で運動方程式に適応するために\(t\)の2階微分を考えると、
慣性系\(S\)における運動方程式の変形
系\(S\)を慣性系とすると、ニュートンの運動法則より次のような運動方程式が成り立つ。
式(2)に式(1)を代入すると、
左辺の第一項を右辺に移項する。
ここで、\({\bf F}’\)を次のように定義する。
この\({\bf F}’\)を式(3)に代入する。
この運動方程式は、系\(S’\)から見た質点\(m\)の運動方程式である。
式(2)と式(5)の比較と慣性力
式(2)は系\(S\)、式(5)は系\(S’\)から見たときの質点\(m\)の運動方程式である。この2式を比較すると、式(5)の方には余計な力\(-{\bf F}’\)が加わることがわかる。
この\(-{\bf F}’\)は式(2)には含まれず、実際に質点には加わっていない力である。このような見かけ上の力を慣性力とよぶ。
ガリレイの相対性原理の証明
ガリレイの相対性原理は、等速かつ平行に移動している系でもニュートンの運動法則が成立するというものであった。つまり、系\(S’\)が等速かつ平行に動くときの慣性力が0になることを証明できれば、式(5)に\(-{\bf F}’=0\)を代入できるため、系\(S’\)における慣性力を含まないニュートンの運動法則が現れる。
系\(S’\)が速度\(\bf V\)で等速かつ平行に動くということは、系\(S’\)の原点が速度\(\bf V\)で等速直線運動することになる。これは、系\(S’\)の原点の加速度が0であることを意味する。したがって、式(4)の慣性力の定義より、この場合の慣性力は0になる。
以上より、ガリレイの相対性原理を証明できた。
ガリレイ変換とは
系\(S'(O’-x’,y’,z’)\)が、系\(S(O-x,y,z)\)に対して、速度\(v\)でx軸方向に動いているとする。このとき、それぞれの成分の関係は次のように表される。
$$x=x’+vt$$$$y=y’$$
$$z=z’$$
このような、2つの系の相対速度が一定の場合における各成分の変換を、ガリレイ変換という。
まとめ
・相対速度とガリレイ変換について説明した。
参考文献
・戸田盛和(1982)『力学〔物理入門コース1〕』,岩波書店.

