質量\(m\)の粒子と質量\(M\)の粒子間に働く万有引力は、物体間の距離が\(r\)のとき、次のように表される。
$$f(r)=-G\frac{mM}{r^2}$$
\(G=6.672×10^{-11}[N・m^2/kg^2]\):万有引力定数
万有引力によるポテンシャル
ポテンシャルエネルギー(位置エネルギー)と力には、次のような関係が成り立つ。
$$f(r)=-\frac{dU}{dr}$$
したがって、ポテンシャルエネルギー\(U(r)\)を求めるには、力を位置で積分すればよい。これを万有引力に適応すると、万有引力によるポテンシャルエネルギー\(U(r)\)は、次のように表せる。
$$U(r)=-G\frac{mM}{r} \cdots (1)$$
ポテンシャルの解釈とブラックホール
上にある通り、万有引力のポテンシャルエネルギーは負になる。これをグラフにすると、下の図のようになる。
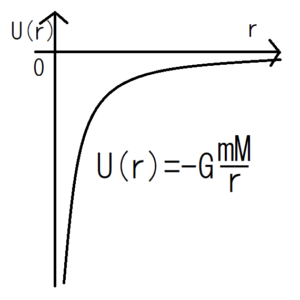
ポテンシャルエネルギーは、その地点での物体の動きやすさを表している。ポテンシャルが低い位置ほど物体は動きやすい。つまり、地球がつくるポテンシャルを考えると、地球の中心(r=0)に近いほど、物体は地球の中心方向に動きやすいということになる。逆に、地球の中心から離れるにつれて、地球がつくるポテンシャルの影響が小さくなっていく。
ただ、\(r=0\)に近づいていくと、ポテンシャルは\(-∞\)に発散してしまう。ということは、これ以上\(r=0\)に近づいたら、ポテンシャルが急すぎて脱出できなくなる場所があるのではなかろうか。実は、これがブラックホールの仕組みである。
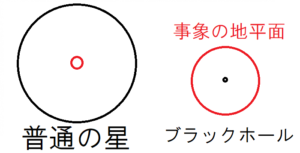
上の図の黒い円は天体本体、赤い円はこれ以上内側に入ったら光でさえ脱出できなくなるという範囲を表している。地球や太陽などの普通の星は、左のように、天体本体が赤い円を含んでいる。そのため、地球の表面から、ロケットなどで地球から脱出することができる。
一方ブラックホールは、あまりにも密度が大きすぎるため、赤い円が天体本体よりも大きくなっている。そのため、天体の表面に到着するよりも先に赤い円に到達してしまう。ブラックホールにおけるこの赤い円を、事象の地平面という。
例題1 重力の大きさ
体重\(60kg\)の人にかかる重力の大きさは何\(N\)か。ただし、地球の重さを\(6.0×10^{24}[kg]\)、半径を\(R=6.4×10^6[m]\)とする。
人が地球の表面にいると仮定して、万有引力の式に代入すればよい。
ちなみに、\(F=mg\)に\(m=60[kg]\)、\(g=9.8\)(重力加速度)を代入すると、人にかかる力は次のようになる。
$$F=60×9.8≒5.9×10^2[N]$$
このように、万有引力から求めた人と地球の間に働く力と、\(F=mg\)から求めた力が一致することがわかる。
例題2 脱出速度
地球からロケットを使って脱出したい。ロケットを地表に対して垂直に打ち上げるとき、最低どれくらいの初速が必要か。
脱出速度を求める問題である。ロケットの質量を\(m\)とおくと、ロケットの力学的エネルギーは次のようになる。
地表にいるときの力学的エネルギーは、求める初速を\(v_0\)、地球の半径を\(R\)とすると、次のようになる。
一方ロケットが無限遠で速度0になった場合、無限遠におけるポテンシャルは式(1)より0だから、このときのロケットの力学的エネルギーは\(0\)になる。
よって、力学的エネルギー保存の法則より、次の式が求められる。
これを\(v_0\)について解く。
よって、脱出速度はおよそ秒速11kmである。途中でロケットの質量\(m\)が消えるので、脱出速度はロケットの質量によらないことがわかる。
参考文献
・戸田盛和(1982)『力学 (物理入門コース1)』,岩波書店.

